已知集合
，集合
，则
（ ）
A． |
B． |
C． |
D． |
设复数
（
是虚数单位），则
（ ）
A． |
B． |
C． |
D． |
已知正项等比数列
中，
，
，则
（ ）
| A．6 | B． |
C． |
D．8 |
已知向量
，
满足
，
，则
（ ）
| A．1 | B．2 | C． |
D． |
给定
：函数
向右平移
个单位后为偶函数的充要条件是
；
：命题“若
，则
”的否命题是“若，则
”．
则下列各命题中，真命题的是
A． |
B． |
C． |
D． |
如图为由三棱柱切割而得到的几何体的三视图，则该几何体的体积为（ ）
A． |
B． |
C． |
D． |
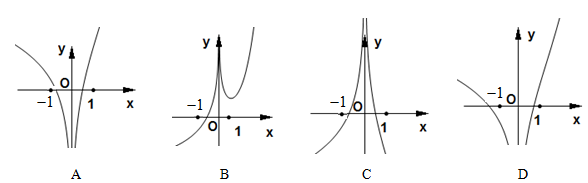
函数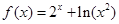
的图象大致为（ ）
已知实数
满足
，则
的最大值为（ ）
A． |
B． |
C． |
D． |
已知抛物线
与双曲线
有共同的焦点
，
为坐标原点，
在
轴上方且在双曲线上，则
的最小值为（ ）
A． |
B． |
C． |
D． |
设
与
是定义在同一区间
上的两个函数，若对任意的
，都有
（
），则称和在上是“
度和谐函数”，
称为“度密切区间”，设
与
在
上是“
度和谐函数”，则
的取值范围是（ ）
A． |
B． |
C． |
D． |
函数
在点
处的切线方程为 。
若正实数x、y满足条件
，则
的最小值为 ．
已知平面区域
恰好被面积最小的圆
及其内部所覆盖，则圆
的方程为 ．
设函数
，若
为奇函数，则
=__________．
给出下面5个命题，
①函数
的最小正周期是
．
②函数
在区间
内是增函数;
③在同一坐标系中，函数
的图象和函数
的图象有3个公共点．
④以双曲线
的右焦点为圆心，且与其渐近线相切的圆的半径为4．
其中真命题的序号为 （写出所有真命题的序号）
设函数
，其中向量
，
，
．
（Ⅰ）求函数
的最大值和单调递增区间；
（Ⅱ）将函数的图象沿x轴进行平移，使平移后得到的图象关于坐标原点成中心对称，如何进行平移使其平移长度最小？
山东省实验中学为了活跃师生的课外文化生活，在2015年3月中旬举办了一次知识竞赛，经过层层筛选，最后五名同学进入了总决赛．在进行笔答题知识竞赛中，最后一个大题是选做题，要求参加竞赛的五名选手从2道题中选做一道进行解答，假设这5位选手选做每一题的可能性均为
，求
（Ⅰ）其中甲乙2位选手选做同一道题的概率．
（Ⅱ）设这5位选手中选做第1题的人数为x，求x的分布列及数学期望．
下图是一几何体的直观图、主视图、俯视图、左视图．
（Ⅰ）若
为
的中点，求证：
面
；
（Ⅱ）证明：
∥面
；
（Ⅲ）求面与面
所成的二面角（锐角）的余弦值．
设函数
，数列
满足
（Ⅰ）求数列
的通项公式；
（Ⅱ）记
试比较
与Q的大小关系，并说明理由．
已知
在点
处的切线方程与直线
垂直．
（Ⅰ）若
，
恒成立，求实数
的取值范围．
（Ⅱ）当
时，求证：
．
已知
，直线l：y=－2，动点P到直线l的距离为d，且d=
．
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）直线m：y=
与点P的轨迹交于M、N两点，当
时，求直线m的倾斜角α的取值范围；
（Ⅲ）设直线h与点P的轨迹交于C、D两点，写出命题“如果直线h过点B，那么
=－12”的逆命题，并判断该逆命题的真假，请说明理由．