【改编】已知复数 ,
, ,若
,若 ,则
,则 所对应点的坐标为( )
所对应点的坐标为( )
A. |
B. |
C. |
D. |
若集合 ,集合
,集合 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
【改编】函数 的定义域为( )
的定义域为( )
A. |
B. |
C. |
D. |
【改编】已知命题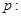
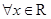 ,
,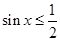 ,则( )
,则( )
A.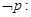 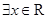 , ,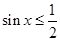 假命题 假命题 |
B.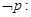 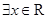 , ,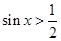 真命题 真命题 |
C.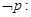 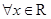 , ,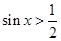 假命题 假命题 |
D.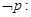 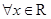 , ,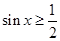 真命题 真命题 |
【原创】若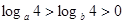 ,则( )
,则( )
A. |
B. |
C. |
D. |
函数 的大致图象为
的大致图象为
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,若点
,若点 的坐标满足
的坐标满足 ,则
,则 的最大值为( )
的最大值为( )
A. |
B. |
C. |
D. |
若 是
是 的重心,
的重心, ,
, ,
, 分别是角
分别是角 的对边,若
的对边,若 ,则角
,则角 ( )
( )
A. |
B. |
C. |
D. |
甲、乙两名运动员的5次测试成绩如下图所示

设s1,s2分别表示甲、乙两名运动员测试成绩的标准差, ,
, 分别表示甲、乙两名运动员测试成绩的平均数,则有( )
分别表示甲、乙两名运动员测试成绩的平均数,则有( )
A. = = ,s1<s2 ,s1<s2 |
B. = = ,s1>s2 ,s1>s2 |
C. > > ,s1>s2 ,s1>s2 |
D. = = ,s1=s2 ,s1=s2 |
设函数 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使 对 一切实数x均成 立,则称
对 一切实数x均成 立,则称 为“倍约束函数”,现给出下列函数:
为“倍约束函数”,现给出下列函数:
① :
:
② :
:
③ ;
;
④
⑤ 是定义在实数集R上的奇函数,且对一切
是定义在实数集R上的奇函数,且对一切 均有
均有 ,
,
其中是“倍约束函数”的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
下图程序执行后输出的T的值是 。

【原创】已知 ,
, ,则
,则 的值为____________.
的值为____________.
已知四棱锥,它的底面是边长为 的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有 个,该四棱锥的体积为 .
的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有 个,该四棱锥的体积为 .


设圆 的半径为
的半径为 ,圆心在
,圆心在
 (
( )上,若圆
)上,若圆 与圆
与圆 相交,则圆心
相交,则圆心 的横坐标的取值范围为 .
的横坐标的取值范围为 .
我们把离心率 的双曲线
的双曲线 称为黄金双曲线.如图是双曲线
称为黄金双曲线.如图是双曲线 的图象,给出以下几个说法:
的图象,给出以下几个说法:
①双曲线 是黄金双曲线;
是黄金双曲线;
②若 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
③若 为左右焦点,
为左右焦点, 为左右顶点,
为左右顶点, (0,
(0, ),
), (0,﹣
(0,﹣ )且
)且 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
④若 经过右焦点
经过右焦点 且
且 ,
, ,则该双曲线是黄金双曲线.
,则该双曲线是黄金双曲线.
其中正确命题的序号为_________ .
(本小题满分12分)2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:


(Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在 [8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
【改编】(本小题满分12分)已知向量
(1)当 时,求
时,求 的值;
的值;
(2)求 在
在 上的单调性
上的单调性
(本小题满分12分)如图,四边形 是正方形,△
是正方形,△ 与△
与△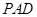 均是以
均是以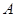 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点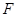 是
是 的中点,点
的中点,点 是边
是边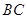 上的任意一点.
上的任意一点.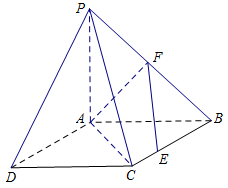
(1)求证: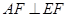 ;
;
(2)求二面角 的平面角的正弦值.
的平面角的正弦值.
(本小题满分12分)已知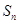 是等差数列
是等差数列 的前n项和,数列
的前n项和,数列 是等比数列,
是等比数列,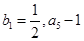 恰为
恰为 的等比中项,圆
的等比中项,圆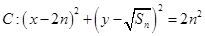 ,直线
,直线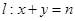 ,对任意
,对任意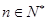 ,直线
,直线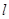 都与圆C相切.
都与圆C相切.
(Ⅰ)求数列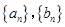 的通项公式;
的通项公式;
(Ⅱ)若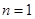 时,
时,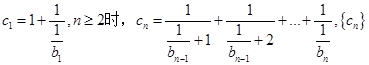 的前n项和为
的前n项和为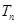 ,求证:对任意
,求证:对任意 ,都有
,都有
(本小题满分13分)已知椭圆C: (a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程.
(2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
②当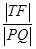 最小时,求点T的坐标.
最小时,求点T的坐标.
设函数 的定义域是
的定义域是 ,其中常数
,其中常数 .
.
(1)若 ,求
,求 的过原点的切线方程.
的过原点的切线方程.
(2)当 时,求最大实数
时,求最大实数 ,使不等式
,使不等式 对
对 恒成立.
恒成立.
(3)证明当 时,对任何
时,对任何 ,有
,有 .
.