【改编】设集合 ,集合
,集合 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
复数 为纯虚数,则实数
为纯虚数,则实数
A. |
B. |
C.2 | D. |
若函数 ,
, 分别是R上的奇函数,偶函数,且满足
分别是R上的奇函数,偶函数,且满足 ,则有
,则有
A. |
B. |
C. |
D. |
设 ,
, 是双曲线
是双曲线
 ,
, 的左、右两个焦点,若双曲线右支上存在一点
的左、右两个焦点,若双曲线右支上存在一点 ,使
,使 (
( 为坐标原点),且
为坐标原点),且 ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )
A. |
B. |
C. |
D. |
现有8名青年,其中5名能任英语翻译工作,4名能胜任电脑软件设计工作,且每人至少能胜这两项工作中的一项,现从中选5人,承担一项任务,其中3人从事英语翻译工作,2人从事软件设计工作,则不同的选派方法有
| A.60种 | B.54种 |
| C.30种 | D.42种 |
定义运算“ ”为:
”为: .若函数
.若函数 ,则该函数的图象大致是( ).
,则该函数的图象大致是( ).

执行如图中的程序框图,若输出的结果为21,则判断框中应填( )

A. |
B. |
C. |
D. |
【改编】已知 ,且满足
,且满足 ,则
,则 的值( )
的值( )
A. |
B.- |
C. |
D. |
给定区域D ,令点集
,令点集 是
是 在D上取得最大值或最小值的点
在D上取得最大值或最小值的点 ,则
,则 中的点最多能确定三角形的个数为( )
中的点最多能确定三角形的个数为( )
| A.15 | B.25 | C.28 | D.32 |
抛物线 (
( )的焦点为
)的焦点为 ,已知点
,已知点 ,
, 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足
 .过弦
.过弦 的中点
的中点 作抛物线准线的垂线
作抛物线准线的垂线 ,垂足为
,垂足为 ,则
,则 的最大值为( )
的最大值为( )
A. |
B.1 | C. |
D.2 |
【改编】 展开式的常数项为 .
展开式的常数项为 . (用数字作答)
(用数字作答)
【原创】已知某几何体的三视图如图所示,则该几何体的外接球的体积为__________.
【原创】已知命题
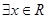 ,
,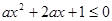 .若命题
.若命题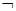
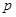 是真命题,则实数
是真命题,则实数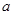 的取值范围是 .
的取值范围是 .
在锐角三角形ABC,A、B、C的对边分别为a、b、c,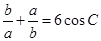 ,则
,则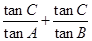 =_______.
=_______.
已知函数
 ,若函数
,若函数 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数 的取值范围为 .
的取值范围为 .
在2014年11月4日宜宾市举办的四川省第十四届少数民族传统体育运动会的餐饮点上,某种茶饮料一天的销售量与该天的日平均气温(单位:℃)有关,若日平均气温不超过15 ℃,则日销售量为100瓶;若日平均气温超过15℃但不超过20 ℃,则日销售量为150 瓶;若日平均气温超过20 ℃,则日销售量为200瓶.据宜宾市气象部门预测,该地区在运动会期间每一天日平均气温不超过15 ℃,超过15 ℃但不超过20 ℃,超过20 ℃这三种情况发生的概率分别为 ,又知P1,P2为方程5x2-3x+a=0的两根,且
,又知P1,P2为方程5x2-3x+a=0的两根,且 .
.
(1)求P1,P2,P3的值;
(2)记ξ表示该茶饮料在运动会期间任意两天的销售量总和(单位:瓶),求 的分布列及数学期望.
的分布列及数学期望.
【改编】(本小题满分12分)函数 部分图象如图所示.
部分图象如图所示.
(Ⅰ)求 的最小正周期及解析式;
的最小正周期及解析式;
(Ⅱ)设 ,求函数
,求函数 在区间
在区间 上的单调性.
上的单调性.
(本题12分)已知数列 的前
的前 项和为
项和为 ,且
,且 ,其中
,其中
(1)求数列 的通项公式;
的通项公式;
(2)若 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:
(本小题满分12分)如图,在四棱锥 中,
中, 平面
平面 ,
, ,四边形
,四边形 满足
满足 ,
, 且
且 ,点
,点 为
为 中点,点
中点,点 为
为 边上的动点,且
边上的动点,且 .
.
(1)求证:平面 平面
平面 ;
;
(2)是否存在实数 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,试求出实数
?若存在,试求出实数 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知点F(1,0),圆E: ,点P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.
,点P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.
(1)求动点Q的轨迹Γ的方程;
(2)若直线 与圆O:
与圆O: 相切,并与(1)中轨迹Γ交于不同的两点A、B.当
相切,并与(1)中轨迹Γ交于不同的两点A、B.当 =
= ,且满足
,且满足 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
已知函数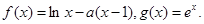
(1)求函数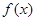 的单调区间;
的单调区间;
(2)当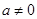 时,过原点分别作曲线
时,过原点分别作曲线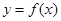 和
和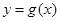 的切线
的切线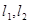 ,已知两切线的斜率互为倒数,证明:
,已知两切线的斜率互为倒数,证明: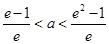 ;
;
(3)设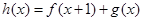 ,当
,当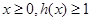 时,求实数
时,求实数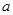 的取值范围.
的取值范围.