已知集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
若复数 为虚数单位)为纯虚数,则实数
为虚数单位)为纯虚数,则实数 的值为( )
的值为( )
A. |
B. |
C. |
D. |
【改编】二项式 的展开式中,
的展开式中, 的系数为( )
的系数为( )
A. |
B. |
C. |
D. |
【原创】要得到函数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )
A.向右平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 |
D.向左平移 个单位 个单位 |
【原创】设 为三条不同的直线,
为三条不同的直线, 为平面,下列命题中说法正确的序号是( )
为平面,下列命题中说法正确的序号是( )
①若 ;
;
②若 ;
;
③若 ;
;
④若 则
则 .
.
| A.①② | B.②③ | C.①④ | D.③④ |
【改编】函数 的图象是( )
的图象是( )

如图,大正方形的面积是34,四个全等三角形围成一个小正方形,直角三角形的较短边长为3,向大正方形内抛撒一枚幸运小花朵,则小花朵落在小正方形内的概率为( )

A. |
B. |
C. |
D. |
若执行下面的程序框图,输出 的值为3,则判断框中应填入的条件是
的值为3,则判断框中应填入的条件是
A. |
B. |
C. |
D. |
已知函数 , 则
, 则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
设定义域为R的函数 若关于x的方程
若关于x的方程 有7个不同的实数解,则m=( ).
有7个不同的实数解,则m=( ).
| A.2 | B.4或6 | C.2或6 | D.6 |
已知函数 的定义域为
的定义域为 ,则函数
,则函数 的定义域是 .
的定义域是 .
如图,茎叶图记录了甲、乙两组各3名同学在期末考试中的数学成绩,则方差较小的那组同学成绩的方差为_______.
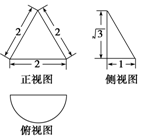
【改编】某几何体的三视图如图所示,其中俯视图是半圆,则该几何体的侧面积为 .
已知变量x,y满足约束条件 ,若
,若 恒成立,则实数
恒成立,则实数 的取值范围为________.
的取值范围为________.
定义两个平面向量的一种运算 ,则关于平面向量上述运算的以下结论中,
,则关于平面向量上述运算的以下结论中,
① ,
,
②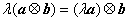 ,
,
③若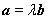 ,则
,则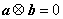 ,
,
④若 且
且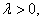 则
则 .
.
恒成立的有 .(填序号 )
(本小题满分12分)从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同。
(1)若抽取后又放回,抽3次,①分别求恰2次为红球的概率及抽全三种颜色球的概率;②求抽到红球次数 的数学期望.
的数学期望.
(2)若抽取后不放回,抽完红球所需次数为 的分布列及期望.
的分布列及期望.
【改编】在 中,角
中,角 的对边分别为
的对边分别为 ,
, 的外接圆半径
的外接圆半径 ,且满足
,且满足 ,
,
(1)求角 和边
和边 的大小;
的大小;
(2)若 是锐角三角形,求
是锐角三角形,求 的面积的取值范围。
的面积的取值范围。
如图,已知四棱锥 中,
中, 是边长为
是边长为 的正三角形,平面
的正三角形,平面 平面
平面 ,四边形
,四边形 是菱形,
是菱形, ,
, 是
是 的中点,
的中点, 是
是 的中点.
的中点.
(Ⅰ)求证: 平面
平面 .
.
(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)设数列 的前
的前 项和为
项和为 ,点
,点 在直线
在直线 上.
上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)在 与
与 之间插入
之间插入 个数,使这
个数,使这 个数组成公差为
个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 项和
项和 ,并求使
,并求使 成立的正整数
成立的正整数 的最大值.
的最大值.
(本小题满分13分)如图,设 为抛物线
为抛物线 的焦点,
的焦点, 是抛物线上一定点,其
是抛物线上一定点,其
坐为 ,
, 为线段
为线段 的垂直平分线上一点,且点
的垂直平分线上一点,且点 到抛物线的准线
到抛物线的准线 的距离为
的距离为 .
.

(Ⅰ)求抛物线的方程;
(Ⅱ)过点P任作两条斜率均存在的直线PA、PB,分别与抛物线交于点A、B,如图示,若直线AB的斜率为定值 ,求证:直线PA、PB的倾斜角互补.
,求证:直线PA、PB的倾斜角互补.
(本小题满分14分)已知函数 ,
, , 其中,
, 其中, 是自然对数的底数.函数
是自然对数的底数.函数 ,
, .
.
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)将 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列 ,求证:
,求证:
(1) ,其中
,其中 ;
;
(2) .
.