若集合 ,则
,则 所含的元素个数为( )
所含的元素个数为( )
| A.0 | B.1 | C.2 | D.3 |
【原创】已知命题
 ,则
,则 为 ( )
为 ( )
A. 真命题 真命题 |
B. 真命题 真命题 |
C. 假命题 假命题 |
D. 假命题 假命题 |
设  ,则
,则  =( )
=( )
| A.-1-i | B.1-i | C.-l+i | D.l+i |
设 是
是 所在平面内一点,
所在平面内一点, 则
则
A. |
B. |
C. |
D. |
已知数列 的首项
的首项 ,
, ,则下列结论正确的是( )
,则下列结论正确的是( )
A.数列是 等比数列 等比数列 |
B.数列 是等比数列 是等比数列 |
C.数列是 等差数列 等差数列 |
D.数列 是等差数列 是等差数列 |
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )

A. |
B. |
C. |
D. |
【改编】某几何体的三视图如图所示,它的表面积为( )

A. |
B. |
C. |
D. |
【改编】若执行下面的程序框图,则输出的k值是( )

| A.4 | B.5 | C.6 | D.7 |
已知双曲线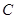 :
: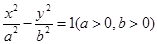 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于
的准线分别交于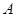 ,
,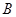 两点,
两点,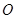 为坐标原点,若双曲线
为坐标原点,若双曲线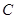 的离心率为2,
的离心率为2,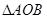 的面积为
的面积为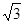 ,则
,则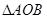 的内切圆半径为( )
的内切圆半径为( )
A.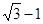 |
B.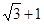 |
C.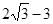 |
D.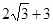 |
已知函数 且
且 有两个零点
有两个零点 、
、 ,则有( )
,则有( )
A. |
B. |
C. |
D. 的范围不确定 的范围不确定 |
有4件不同的产品排成一排,其中A、B两件产品排在一起的不同排法有____种.
函数 的部分图象如图所示,设
的部分图象如图所示,设 为坐标原点,
为坐标原点, 是图象的最高点,
是图象的最高点, 是图象与
是图象与 轴的交点,则
轴的交点,则 __________.
__________.
设数列 满足
满足 ,
, ,则该数列的前
,则该数列的前 项的乘积
项的乘积 _________.
_________.
若 为经过抛物线
为经过抛物线 焦点的弦,且
焦点的弦,且 ,O为坐标原点,则
,O为坐标原点,则 的面积等于_________.
的面积等于_________.
【原创】对定义在区间D上的函数 和
和 ,如果对任意
,如果对任意 ,都有
,都有 成立,那么称函数
成立,那么称函数 在区间D上可被
在区间D上可被 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
① 在区间
在区间 上可被
上可被 替代;
替代;
② 可被
可被 替代的一个“替代区间”为
替代的一个“替代区间”为 ;
;
③ 在区间
在区间 可被
可被 替代,则
替代,则 ;
;
④ ,则存在实数
,则存在实数 ,使得
,使得 在区间
在区间 上被
上被 替代;
替代;
其中真命题的有
(本小题满分12分)某学校举行联欢会,所有参演的节目都由甲、乙、丙三名专业老师投票决定是否获奖.甲、乙、丙三名老师都有“获奖”、“待定”、“淘汰”三类票各一张.每个节目投票时,甲、乙、丙三名老师必须且只能投一张票,每人投三类票中的任何一类票的概率都为 ,且三人投票相互没有影响.若投票结果中至少有两张“获奖”票,则决定该节目最终获一等奖;否则,该节目不能获一等奖.
,且三人投票相互没有影响.若投票结果中至少有两张“获奖”票,则决定该节目最终获一等奖;否则,该节目不能获一等奖.
(1)求某节目的投票结果是最终获一等奖的概率;
(2)求该节目投票结果中所含“获奖”和“待定”票票数之和 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)如图所示,在四边形 中,
中, ,且
,且 ,
, ,
, .
.
(1)求 的面积;
的面积;
(2)若 ,求
,求 的长.
的长.
(本小题满分12分)如图 是图
是图 的三视图,三棱锥
的三视图,三棱锥 中,
中, ,
, 分别是棱
分别是棱 ,
, 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
已知数列 中
中
 .
.
(1)是否存在实数 ,使数列
,使数列 是等比数列?若存在,求
是等比数列?若存在,求 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(2)若 是数列
是数列 的前
的前 项和,求满足
项和,求满足 的所有正整数
的所有正整数 .
.
(本小题满分12分)如图所示,椭圆 :
: ,其中
,其中 ,焦距为
,焦距为 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 交于点
交于点 、
、 ,点
,点 在
在 之间,又点
之间,又点 ,
, 的中点横坐标为
的中点横坐标为 ,且
,且 .
.
(1)求椭圆 的标准方程 ;
的标准方程 ;
(2)求实数 的值.
的值.
(本小题满分14分)已知函数 ,
,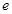 为自然对数的底数.
为自然对数的底数.
(1)过点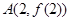 的切线斜率为
的切线斜率为 ,求实数
,求实数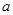 的值;
的值;
(2)当 时,求证:
时,求证: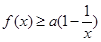 ;
;
(3)在区间 上
上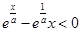 恒成立,求实数
恒成立,求实数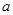 的取值范围.
的取值范围.