下列命题中正确的是( )
| A.任意两复数均不能比较大小 |
B.复数 是实数的充要条件是 是实数的充要条件是 |
C.复数 是纯虚数的充要条件是 是纯虚数的充要条件是 |
D. 的共轭复数是 的共轭复数是 |
若某市 所中学参加中学生合唱比赛的得分用茎叶图表示(如图),其中茎为十位数,叶为个位数,则这组数据的中位数是( )
所中学参加中学生合唱比赛的得分用茎叶图表示(如图),其中茎为十位数,叶为个位数,则这组数据的中位数是( )

A. |
B. |
C. |
D. |
已知全集 , 集合
, 集合 ,
,  , 则集合
, 则集合 可以表示为( )
可以表示为( )
A. |
B. |
C. |
D. |
已知 是首项为
是首项为 的等比数列,
的等比数列, 是其前
是其前 项和,且
项和,且 ,则数列
,则数列 前
前 项和为 ( )
项和为 ( )
A. |
B. |
C. |
D. |
【原创】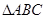 中三边上的高依次为
中三边上的高依次为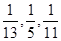 ,则
,则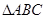 为( )
为( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不存在这样的三角形 |
如图,正方体 的棱长为
的棱长为 ,线段
,线段 上有两个动点
上有两个动点 ,且
,且 ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A. |
B. 平面 平面 |
C.三棱锥 的体积为定值 的体积为定值 |
D. 的面积与 的面积与 的面积相等 的面积相等 |
若 则
则 的取值范围是( )
的取值范围是( )
A.(0,  ] ] |
B.[0,  ] ] |
C.[0,  - - ] ] |
D.[0,  + + ] ] |
执行如下图所示的程序框图,如果输入t [-2, 2],则输出的s属于( )
[-2, 2],则输出的s属于( )
| A.[-6, -2] | B.[-5, -1] | C.[-4, 5] | D.[-3, 6] |
【改编题】若直线 ,始终平分圆
,始终平分圆 的周长,则
的周长,则 的最小值为 ( )
的最小值为 ( )
| A.1 | B. |
C. |
D.6 |
已知函数 有两个极值点
有两个极值点 ,
, ,且
,且 ,则( )
,则( )
A. |
B. |
C. |
D. |
【原创】已知 ,则
,则 的值为_______________.
的值为_______________.
已知函数 在
在 是单调函数,则实数
是单调函数,则实数 的取值范围是 .
的取值范围是 .
【改编题】过抛物线 的焦点
的焦点 的直线
的直线 与抛物线在第一、四象限分别交于
与抛物线在第一、四象限分别交于 两点,且
两点,且 ,则线段
,则线段 的中点到该抛物线准线的距离为__________.
的中点到该抛物线准线的距离为__________.
在平面直角坐标系中,O为坐标原点,A(1,0),B(0,3),C(3,0),动点D满足 ,则
,则 的最小值是__________.
的最小值是__________.
设函数 的定义域为
的定义域为 ,如果存在非零常数
,如果存在非零常数 ,对于任意
,对于任意 ,都有
,都有 ,则称函数
,则称函数 是“似周期函数”,非零常数
是“似周期函数”,非零常数 为函数
为函数 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数” 的“似周期”为-1,那么它是周期为2的周期函数;
的“似周期”为-1,那么它是周期为2的周期函数;
②函数 是“似周期函数”;
是“似周期函数”;
③函数 是“似周期函数”;
是“似周期函数”;
④如果函数 是“似周期函数”,那么“
是“似周期函数”,那么“ ”.
”.
其中是真命题的序号是 .(写出所有满足条件的命题序号)
(本大题满分12分)在 中,角
中,角 为锐角,已知内角
为锐角,已知内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,向量
,向量 且向量
且向量 共线.
共线.
(1)求角 的大小;
的大小;
(2)如果 ,且
,且 ,求
,求 的值.
的值.
(本大题满分12分)四棱锥 中,
中, ⊥底面
⊥底面 ,
, ,
, ,
, .
.
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
(Ⅱ)若侧棱 上的点
上的点 满足
满足 ,求三棱锥
,求三棱锥 的体积.
的体积.
(本大题满分12分)从某学校的 名男生中随机抽取
名男生中随机抽取 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 ,第二组
,第二组 ,第八组
,第八组 ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为 人.
人.
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在 以上(含
以上(含 )的人数;
)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,事件
,事件 ,事件
,事件 ,求
,求
(本小题满分13分)已知函数
(1)求函数 的单调区间;
的单调区间;
(2)当 时,
时, ,求实数
,求实数 的取值范围
的取值范围
【改编题】(本小题满分13分)各项均为正数的数列 的前
的前 项和为
项和为 ,已知点
,已知点 在函数
在函数 的图象上,且
的图象上,且
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)在 之间插入
之间插入 个数,使这
个数,使这 个数组成公差为
个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 项和
项和 .并求
.并求 的最小值.
的最小值.
(本小题满分13分)已知椭圆 过点
过点 ,两焦点为
,两焦点为 、
、 ,
, 是坐标原点,不经过原点的直线
是坐标原点,不经过原点的直线 与椭圆交于两不同点
与椭圆交于两不同点 、
、 .
.
(1)求椭圆C的方程;
(2)当 时,求
时,求 面积的最大值;
面积的最大值;
(3)若直线 、
、 、
、 的斜率依次成等比数列,求直线
的斜率依次成等比数列,求直线 的斜率
的斜率 .
.