已知 是虚数单位,
是虚数单位, 和
和 都是实数,且
都是实数,且 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
【原创】已知集合 .若
.若 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
四名同学根据各自的样本数据研究变量 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且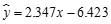 ;
;
②y与x负相关且 ;
;
③y与x正相关且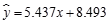 ;
;
④y与x正相关且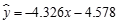 .
.
其中一定不正确的结论的序号是 ( )
| A.①② | B.②③ | C.③④ | D.①④ |
下列命题中,正确的一个是 ( )
A. |
B.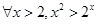 |
C.若 成立的必要不充分条件,则 成立的必要不充分条件,则 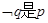 成立的充分不必要条件 成立的充分不必要条件 |
D.若 ,则 ,则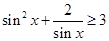 |
【改编题】在边长为2的正方形 内任取一点
内任取一点 ,使点
,使点 到四个顶点的距离至少有一个小于1的概率是( )
到四个顶点的距离至少有一个小于1的概率是( )
A. |
B. |
C. |
D. |
若实数 、
、 满足
满足 ,且
,且 的最大值等于
的最大值等于 ,则正实数
,则正实数 的值等于( )
的值等于( )
A. |
B. |
C. |
D. |
四棱锥的三视图如图所示,则最长的一条侧棱的长度是( )

A. |
B. |
C. |
D. |
已知函数 是定义在
是定义在 上的奇函数,对于任意
上的奇函数,对于任意 ,
, ,
, 总有
总有 且
且 .若对于任意
.若对于任意 ,存在
,存在 ,使
,使 成立,则实数
成立,则实数 的取值范围是( )
的取值范围是( )
A. |
B. 或 或 |
C. 或 或 |
D. 或 或 或 或 |
如图, 、
、 分别是双曲线
分别是双曲线 的两个焦点,以坐标原点
的两个焦点,以坐标原点 为圆心,
为圆心, 为半径的圆与该双曲线左支交于
为半径的圆与该双曲线左支交于 、
、 两点,若△
两点,若△ 是等边三角形,则双曲线的离心率为 ( )
是等边三角形,则双曲线的离心率为 ( )

A. |
B.2 | C. |
D. |
已知等差数列 的首项为
的首项为 ,公差为
,公差为 ,其前n项和为
,其前n项和为 ,若直线
,若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则数列
对称,则数列 的前10项和=( )
的前10项和=( )
A. |
B. |
C. |
D.2 |
若函数 ,则
,则 = _________.
= _________.
【原创】如图,在平行四边形 中,
中, ,
, 分别为
分别为 的中点,
的中点, 分别与
分别与 交于
交于 两点,则
两点,则 =________.
=________.
执行如图所示的流程图,则输出的 为 .
为 .

【改编题】在锐角三角形 中,
中, ,
, ,
, 是三角形
是三角形 的内角,且
的内角,且 ,设函数
,设函数
 ,则
,则 的最大值为 .
的最大值为 .
若函数 满足:存在
满足:存在 ,对定义域内的任意
,对定义域内的任意 恒成立,则称
恒成立,则称 为
为 函数.现给出下列函数:①
函数.现给出下列函数:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤
其中为 函数的序号是 .(把你认为正确的序号都填上)
函数的序号是 .(把你认为正确的序号都填上)
【原创】在 中,内角
中,内角 的对边分别为
的对边分别为 .已知
.已知 =
= .
.
(1)求 的值;
的值;
(2) 若 ,
, 的周长为14,求
的周长为14,求 的长.
的长.
(本小题满分12分)如图,在斜三棱柱 中,侧面
中,侧面 与侧面
与侧面 都是菱形,
都是菱形, ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求四棱锥
,求四棱锥 的体积.
的体积.
某校高二年级的一次数学考试中,为了分析学生的得分情况,随机抽取 名同学的成绩,数据的分组统计表如下:
名同学的成绩,数据的分组统计表如下:
| 分组 |
频数 |
频率 |
频率/组距 |
| (40,50] |
2 |
0.02 |
0.002 |
| (50,60] |
4 |
0.04 |
0.004 |
| (60,70] |
11 |
0.11 |
0.011 |
| (70,80] |
38 |
0.38 |
0.038 |
| (80,90] |
 |
 |
 |
| (90,100] |
11 |
0.11 |
0.011 |
| 合计 |
 |
 |
 |
(1)求出表中 的值;
的值;
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在 中的6位同学中任意抽取2人进行调查,求分数在
中的6位同学中任意抽取2人进行调查,求分数在 和
和 中各有一人的概率.
中各有一人的概率.
已知函数 处的切线l与直线
处的切线l与直线 垂直,函数
垂直,函数
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若函数 存在单调递减区间,求实数
存在单调递减区间,求实数 的取值范围;
的取值范围;
(Ⅲ)设 是函数
是函数 的两个极值点,若
的两个极值点,若 ,求
,求 的最小值.
的最小值.
已知等差数列 的公差不为零,
的公差不为零, ,等比数列
,等比数列 的前3项满足
的前3项满足 .
.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)设 …
… ,是否存在最大整数
,是否存在最大整数 ,使对任意的
,使对任意的 ,均有
,均有 总成立?若存在,求出
总成立?若存在,求出 的值;若不存在,请说明理由
的值;若不存在,请说明理由
(本小题满分13分)已知椭圆 (
( )经过点
)经过点 ,离心率为
,离心率为 ,动点
,动点 (
( ).
).
(1)求椭圆的标准方程;
(2)求以 (
( 为坐标原点)为直径且被直线
为坐标原点)为直径且被直线 截得的弦长为
截得的弦长为 的圆的方程;
的圆的方程;
(3)设 是椭圆的右焦点,过点
是椭圆的右焦点,过点 作
作 的垂线与以
的垂线与以 为直径的圆交于点
为直径的圆交于点 ,证明线段
,证明线段 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.