设全集
，集合
，则
=（ ）
A． |
B． |
C． |
D． |
设 
，则 
=（ ）
| A．-1-i | B．1-i | C．-l+i | D．l+i |
“实数
”是“直线
和直线 
相互平行”的（ ）
| A．充要条件 | B．必要不充分条件 |
| C．充分不必要条件 | D．既不充分也不必要条件 |
某校共有学生
名，各年级男、女生人数如表所示，已知高一、高二年级共有女生
人．现用分层抽样的方法在全校抽取
名学生，则应在高三年级抽取的学生人数为（ ）
| |
高一年级 |
高二年级 |
高三年级 |
| 女生 |
 |
 |
 |
| 男生 |
 |
 |
 |
A．12人 B．16人 C．18人 D．24人
【改编】在△ABC中，已知
，
，
=
，则△ABC的面积为（ ）
A． |
B． |
C． |
D． |
在区间
内随机取两个数分别记为
，则使得函数
有零点的概率为（ ）
A．1- |
B．1- |
C．1-  |
D．1- |
已知函数
，则
= （ ）
A． |
B． |
C．2015 | D．2014 |
【原创】一个几何体的三视图如图所示，则这个几何体的体积为 （ ）
A． |
B． |
C． |
D． |
已知不等式组
，表示的平面区域为M，若直线
与平面区域M有公共点，则k的取值范围是（ ）
A． |
B． |
C． |
D． |
等差数列
的前n项和为
，且满足
，
，则
，
， ，
中最大的项为（ ）
A． |
B． |
C． |
D． |
已知F是双曲线C：
的右焦点，过点F向C的一条渐近线引垂直，垂足为A，交另一条渐近线于点B，若
，则C的离心率是（ ）
A． |
B． |
C． |
D．2 |
已知函数
，若
，则a的取值范围是（ ）
A． |
B． |
C． |
D． |
【改编】已知向量
，
，满足
=2，
，，则
等于 ．
若抛物线
上的两点
、
到焦点的距离之和为6，则线段
的中点到
轴的距离为 ．
【改编】已知函数
的部分图像如图所示，则
的的对称轴为 ．
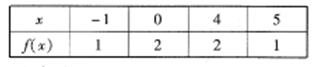
已知函数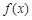
的定义域为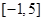
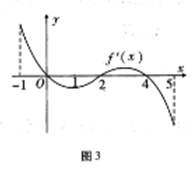
，部分对应值如下表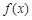，的导函数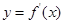
的图象如图3所示．
下列关于函数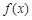的命题：
①函数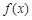的值域为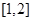
；
②函数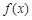在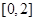
上是减函数；
③如果当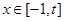
时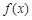，的最大值是2，那么t的最大值为4；
④当
时，函数
有4个零点．
其中真命题为 ．
（本小题满分12分）等差数列
中，
，其前
项和为
．等比数列
的各项均为正数，
，且
，
．
（1）求数列与
的通项公式；
（2）求数列
的前项和
．
（本小题满分12分）如图，矩形
中，
，
，
是
中点，
为
上的点，且
．
（1）求证：
；
（2）求三棱锥
的体积．
【原创】（本小题满分12分）为调查某市高中男生百米成绩，从该市高中男生中随机抽取20名学生进行百米测试，学生成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组
，第二组
第五组
，如图是按上述分组方法得到的频率分布直方图．根据有关规定，成绩小于16秒为达标．
（Ⅰ）求这组数据的众数、中位数及达标率（精确到0．01）；
（Ⅱ）从这20人中不达标的人员中任取3人，至少二人成绩在16～17之间的概率．
【改编】（本小题满分12分）已知椭圆C：
过点
，且椭圆C的离心率为
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）
为坐标原点，斜率为
的直线过
点，且与点
的轨迹交于点
，
，若
，求△
的面积．
（本小题满分12分）已知函数
，其中
。
（Ⅰ）讨论函数
的单调性；
（Ⅱ）若不等式
在
上恒成立，求实数
的取值范围。
已知圆内接△ABC中，D为BC上一点，且△ADC为正三角形，点E为BC的延长线上一点，AE为圆O的切线．
（Ⅰ）求∠BAE 的度数；
（Ⅱ）求证：
选修4—5： 不等式选讲．
（Ⅰ）设函数
．证明：
；
（Ⅱ）若实数
满足
，求证：