若集合 ,则
,则 所含的元素个数为( )
所含的元素个数为( )
| A.0 | B.1 | C.2 | D.3 |
设 (
( 是虚数单位),则复数
是虚数单位),则复数 对应的点位于( )
对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
设 均为非零向量,下列四个条件中,使
均为非零向量,下列四个条件中,使 成立的必要条件是( ).
成立的必要条件是( ).
A. |
B. |
C. |
D. 且 且 |
已知某锥体的正视图和侧视图如图2,其体积为 ,则该锥体的俯视图可以是( )
,则该锥体的俯视图可以是( )


已知不等式组 ,表示的平面区域为M,若直线
,表示的平面区域为M,若直线 与平面区域M有公共点,则k的取值范围是( )
与平面区域M有公共点,则k的取值范围是( )
A. |
B. |
C. |
D. |
若某程序框图如图所示,则该程序运行后输出的B等于( )

| A.63 | B.31 | C.15 | D.7 |
已知函数 ,有一个零点为
,有一个零点为 ,则
,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
已知数列 为等比数列,且
为等比数列,且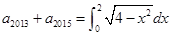 ,则
,则 的值为( )
的值为( )
A.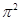 |
B.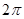 |
C. |
D.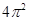 |
如图,矩形ABCD的四个顶点的坐标分别为A(0,—1),B( ,—1),C(
,—1),C( ,1),D(0,1),正弦曲线
,1),D(0,1),正弦曲线 和余弦曲线
和余弦曲线 在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( ).
在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( ).

A. |
B. |
C. |
D. |
已知三棱锥 的所有顶点都在球
的所有顶点都在球 的球面上,
的球面上, 是边长为
是边长为 的正三角形,
的正三角形,  为球
为球 的直径,且
的直径,且 ;则此棱锥的体积为( )
;则此棱锥的体积为( )
A. |
B. |
C. |
D. |
【原创题】若双曲线 的焦点在
的焦点在 轴上,过点
轴上,过点 作圆
作圆 的切线,切点分别为
的切线,切点分别为 ,直线
,直线 恰好经过
恰好经过 点,则双曲线方程为( )
点,则双曲线方程为( )
A. |
B. |
C. |
D. |
【原创题】若关于 的不等式
的不等式 对任意实数
对任意实数 恒成立,则
恒成立,则 的最大值为( )
的最大值为( )
A. |
B. |
C. |
D. |
【改编题】二项式 的展开式中的常数项是
的展开式中的常数项是 ,则实数
,则实数 的值 .
的值 .
己知函数 ,
, 为
为 的等差数列,则
的等差数列,则 _____________.
_____________.
【改编题】已知[x]表示不超过实数x的最大整数(x∈R),如:[﹣1.3]=﹣2,[0.8]=0,[3.4]=3.定义{x}=x﹣[x],求{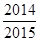 }+{
}+{ }+{
}+{ }+…+{
}+…+{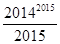 }=
}=
设 的三边长分别为
的三边长分别为 ,
, ,
, ,
, ,
, ,
, ,
, ,若
,若 ,
, ,
, ,
, ,
, ,则
,则 的最大值是 .
的最大值是 .
已知函数 部分图象如图所示。
部分图象如图所示。
(1)求函数 的解析式;
的解析式;
(2)当 时,求函数
时,求函数 的值域。
的值域。
小王在某社交网络的朋友圈中,向在线的甲、乙、丙随机发放红包,每次发放1个.
(Ⅰ)若小王发放5元的红包2个,求甲恰得1个的概率;
(Ⅱ)若小王发放3个红包,其中5元的2个,10元的1个.记乙所得红包的总钱数为X,求X的分布列和期望.
如图,在边长为 的菱形
的菱形 中,
中, ,点
,点 ,
, 分别是边
分别是边 ,
, 的中点,
的中点, ,沿
,沿 将△
将△ 翻折到△
翻折到△ ,连接
,连接 ,得到如图的五棱锥
,得到如图的五棱锥 ,且
,且 .
.
(1)求证: 平面
平面 ;
;
(2)求二面角 的正切值.
的正切值.
已知椭圆C: 过点
过点 ,且椭圆C的离心率为
,且椭圆C的离心率为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若动点P在直线 上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线
上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线 .证明:直线
.证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
)已知函数
(1)若直线 过点
过点 ,并且与曲线
,并且与曲线 相切,求直线
相切,求直线 的方程;
的方程;
(2)设函数 在
在 上有且只有一个零点,求
上有且只有一个零点,求 的取值范围。(其中
的取值范围。(其中 为自然对数的底数)
为自然对数的底数)
选修4-1:几何证明选讲
如图所示,圆 的两弦
的两弦 和
和 交于点
交于点 ,
, ∥
∥ ,
, 交
交 的延长线于点
的延长线于点 ,
, 切圆
切圆 于点
于点 .
.
(1)求证:△ ∽△
∽△ ;
;
(2)如果 ,求
,求 的长.
的长.
选修4—4:坐标系与参数方程
坐标系与参数方程在直角坐标系xOy中,圆C的参数方程 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)射线 与圆C的交点为O、P两点,求P点的极坐标.
与圆C的交点为O、P两点,求P点的极坐标.
选修4—5:不等式选讲
已知函数 ,
, .
.
(Ⅰ)当 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)设 ,且当
,且当 时,
时, ,求a的取值范围.
,求a的取值范围.