已知 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
【改编题】如图,在复平面内,复数 和
和 对应的点分别是
对应的点分别是 和
和 ,若
,若 ,则
,则 对应复平面中的点在( )
对应复平面中的点在( )

| A.第一象限 | B.第二复限 | C.第三象限 | D.第四象限 |
下列说法正确的是
| A.样本10,6,8,5,6的标准差是3.3; |
B.“ 为真”是“ 为真”是“ 为真”的充分不必要条件; 为真”的充分不必要条件; |
C.已知点 在抛物线 在抛物线 的准线上,记其焦点为F,则直线AF的斜率等于 的准线上,记其焦点为F,则直线AF的斜率等于 |
D.设有一个回归直线方程为 ,则变量 ,则变量 每增加一个单位, 每增加一个单位, 平均减少1.5个单位; 平均减少1.5个单位; |
已知两条不同直线 ,
, ,三个不同平面
,三个不同平面 ,
, ,
, ,下列命题中正确是( )
,下列命题中正确是( )
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , ,则 ,则 |
【改编题】如图是某几何体的三视图,则该几何体的体积等于 ,则图中的
,则图中的 的值( )
的值( )

A. |
B. |
C.1 | D. |
如果直线 与
与 轴正半轴,
轴正半轴, 轴正半轴围成的四边形封闭区域(含边界)中的点,使函数
轴正半轴围成的四边形封闭区域(含边界)中的点,使函数 的最大值为8,求
的最大值为8,求 的最小值( )
的最小值( )
| A.4 | B.3 | C.2 | D.0 |
已知函数 ,则它们的图象可能是( )
,则它们的图象可能是( )

已知函数 (
( )的一条对称轴是
)的一条对称轴是 ,则函数
,则函数 的最小正周期不可能是( )
的最小正周期不可能是( )
A. |
B. |
C. |
D. |
若 和
和 是计算机在区间
是计算机在区间 上产生的随机数,那么函数
上产生的随机数,那么函数 的值域为
的值域为 (实数集)的概率为( )
(实数集)的概率为( )
A. |
B. |
C. |
D. |
【原创题】已知函数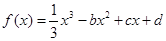 ,设曲线
,设曲线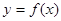 过点
过点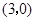 ,且在点
,且在点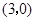 处的切线的斜率等于
处的切线的斜率等于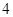 ,
,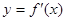 为
为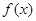 的导函数,满足
的导函数,满足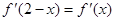 ;则
;则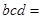 ( )
( )
A.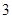 |
B.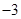 |
C. |
D.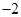 |
【改编题】已知椭圆 ,以O为圆心,短半轴长为半径作圆O,过椭圆的长轴的一端点P作圆O的两条切线,切点为A、B,若
,以O为圆心,短半轴长为半径作圆O,过椭圆的长轴的一端点P作圆O的两条切线,切点为A、B,若 ,且
,且 ,则椭圆的离心率为( )
,则椭圆的离心率为( )

A. B.
B. C.
C. D.
D.
已知函数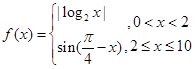 ,若存在实数
,若存在实数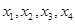 ,且
,且 则
则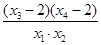 的取值范围是( )
的取值范围是( )
| A.(0,12) | B.(4.16) | C.(9,21) | D.(15,25) |
在二项式 的展开式中各项系数之和为
的展开式中各项系数之和为 ,各项二项式系数之和为
,各项二项式系数之和为 ,且
,且 ,则展开式中含
,则展开式中含 项的系数为 .
项的系数为 .
执行如图所示的程序框图,输出的x值为
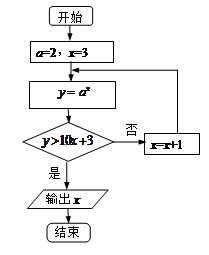
已知 N
N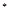 ,且
,且 ,
, C
C C
C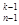 ,则可推出
,则可推出
C C
C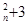 C
C C
C C
C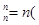 C
C C
C
 C
C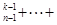 C
C
 ,
,
由此,可推出C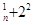 C
C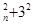 C
C C
C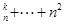 C
C .
.
数列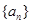 的前n项和为
的前n项和为 ,
,
 ,若
,若 ,则
,则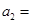 .
.
某同学用“五点法”画函数 在某一个周期的图象时,列表并填入的部分数据如下表:
在某一个周期的图象时,列表并填入的部分数据如下表:
(1)求 ,
, ,
, 的值及函数
的值及函数 的表达式;
的表达式;
(2)将函数 的图象向左平移
的图象向左平移 个单位,可得到函数
个单位,可得到函数 的图象,求函数
的图象,求函数 在区间
在区间 的最小值.
的最小值.
为了解甲、乙两厂的产品质量,分别从两厂生产的产品中各随机抽取10件,测量产品中某种元素的含量(单位:毫克),其测量数据的茎叶图如下:
规定:当产品中此种元素含量大于18毫克时,认定该产品为优等品。
(1)试比较甲、乙两厂生产的产品中该种元素含量的平均值的大小;
(2)从乙厂抽出上述10件产品中,随机抽取3件,求抽到的3件产品中优等品数 的分布列及数学期望。
的分布列及数学期望。
如图,在边长为 的菱形
的菱形 中,
中, ,点
,点 ,
, 分别是边
分别是边 ,
, 的中点,
的中点, ,沿
,沿 将△
将△ 翻折到△
翻折到△ ,连接
,连接 ,得到如图的五棱锥
,得到如图的五棱锥 ,且
,且 .
.
(1)求证: 平面
平面 ;
;
(2)求二面角 的正切值.
的正切值.
已知抛物线 的焦点为F,点P是抛物线上的一点,且其纵坐标为4,
的焦点为F,点P是抛物线上的一点,且其纵坐标为4, .
.
(1)求抛物线的方程;
(2)设点 ,
, (
( )是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
)是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
设函数 
(Ⅰ)若 ,是否存在k和m,使得
,是否存在k和m,使得  ,
, ,若存在,求出k和m的值,若不存在,说明理由
,若存在,求出k和m的值,若不存在,说明理由
(Ⅱ)设  有两个零点
有两个零点  ,且
,且  成等差数列,
成等差数列,  是 G (x)的导函数,求证:
是 G (x)的导函数,求证: 
选修4-1:几何证明选讲
如图所示,已知 为圆
为圆 的直径,
的直径, ,
, 是圆
是圆 上的两个点,
上的两个点, 于
于 ,
, 交
交 于
于 ,交
,交 于
于 ,
, .
.
(1)求证: 是劣弧
是劣弧 的中点;
的中点;
(2)求证: .
.
选修4—4:坐标系与参数方程
已知直线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程是
的极坐标方程是 .
.
(1)写出直线 的极坐标方程与曲线
的极坐标方程与曲线 的普通方程;
的普通方程;
(2)若点 是曲线
是曲线 上的动点,求
上的动点,求 到直线
到直线 距离的最小值,并求出此时
距离的最小值,并求出此时 点的坐标.
点的坐标.
选修4—5:不等式选讲
设函数 .
.
(Ⅰ)解不等式 ;
;
(Ⅱ)若 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.