已知集合
，则 
A． |
B．{1} | C．[0，1] | D． |
已知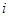
是虚数单位，
、
，则“
”是“
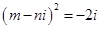”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
已知双曲线 
的一条渐近线方程是 
，它的一个焦点在抛物线 
的准线上，则双曲线线的方程为
A． |
B． |
C． |
D． |
函数
的图象可能是
已知某几何体的三视图（单位：
）如图所示，则该几何体的体积是（ ）
A． |
B． |
C． |
D． |
在直角梯形ABCD中，
，
，
，则
（ ）
A． |
B． |
C． |
D． |
4名大学生到三家企业应聘，每名大学生至多被一家企业录用，则每家企业至少录用一名大学生的情况有（ ）
| A．24种 | B．36种 | C．48种 | D．60种 |
设偶函数
的部分图象如图所示，
为等腰直角三角形，
，
，则
的值为（ ）
（A）
（B）
（C）
（D）
【改编题】设偶函数的部分图象如图所示，
， ，
，则的值为（ ）
（A） （B） （C） （D）
三棱柱
侧棱与底面垂直，体积为
，高为
，底面是正三角形，若
是
中心，则
与平面
所成的角大小是（ ）
A． |
B． |
C． |
D． |
已知函数
的导函数为 
，满足 
，且
，则的单调性情况为（ ）
| A．先增后减 | B．单调递增 | C．单调递减 | D．先减后增 |
【原创题】已知椭圆
的，右焦点
，过椭圆右焦点斜率为
的直线
与椭圆C相交于
两点，
为椭圆的右顶点，直线
分别交直线
于点
，线段
的中点为
，记直线
的斜率为
，则
的值为（ ）
A．
B．
C．
D不确定
【原创题】设
表示不小于
的最小整数，如
，若函数
，则函数
的值域为（ ）
A． |
B． |
C． |
D． |
设函数
则
时，
表达式中的展开式中的常数项为 ．（用数字作答）
【改编题】运行如图所示的流程图，如果输入
，且输出的
，则输入正数
的值为 ．
【改编题】已知抛物线
的焦点为
，过射线交
轴于
，与抛物线
相交与点
，与其准线相交于点
，若
，则的坐标为 ．
已知定义在R上的函数f(x)的图象连续不断，若存在常数
，
使得
对任意的实数x成立，则称f(x)是回旋函数．
给出下列四个命题：
①常值函数
为回旋函数的充要条件是t= -1;
②若
为回旋函数，则t>l;
③函数
不是回旋函数；
④若f(x)是t=2的回旋函数，则f(x)在[0,4030]上至少有2015个零点．
其中为真命题的是_________（写出所有真命题的序号）．
已知函数
．
（1）求函数的最小正周期、最大值及取最大值时自变量的取值集合；
（2）在△ABC中，角A，B，C的对边分别是a，b，c；若a，b，c成等比数列，且
，求
的值．
某市规定，高中学生三年在校期间参加不少于
小时的社区服务才合格．教育部门在全市随机抽取200位学生参加社区服务的数据，按时间段
，
，
，
，
（单位：小时）进行统计，其频率分布直方图如图所示．
（1）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；
（2）从全市高中学生（人数很多）中任意选取3位学生，记
为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量的分布列和数学期望
．
如图，在四棱锥
中，侧棱
底面
，
，
，
，
，
是棱
中点．
（1）求证：
平面
；
（2）设点
是线段
上一动点，且
，当直线
与平面
所成的角最大时，求
的值．
已知如图，圆
和抛物线
，圆的切线
与抛物线
交于不同的点
，
．
（1）当直线的斜率为
时，求线段
的长；
（2）设点
和点
关于直线
对称，问是否存在圆的切线
使得
？若存在，求出直线的方程；若不存在，请说明理由．
已知函数
，
， 其中，
是自然对数的底数．函数
，
．
（Ⅰ）求
的最小值；
（Ⅱ）将
的全部零点按照从小到大的顺序排成数列
，求证：
（1）
，其中
；
（2）
．
选修4-1：几何证明选讲
如图，点
在圆
直径
的延长线上，
切圆于
点，
的平分线
交
于点
，交
于
点．
（1）求
的度数；
（2）若
，求
．
选修4—4：坐标系与参数方程
在直角坐标系中，以原点为极点，x轴的正半轴为极轴建坐标系,已知曲线
，已知过点
的直线的参数方程为：
（t为参数），直线与曲线C分别交于M，N．
（Ⅰ）写出曲线C和直线的普通方程；
（Ⅱ）若
成等比数列，求a的值．
选修4—5：不等式选讲
已知函数
．
（1）求不等式
的解集；
（2）若关于
的不等式
的解集非空，求实数
的取值范围．