若集合 ,集合
,集合 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
复数 在复平面内对应的点的坐标是( )
在复平面内对应的点的坐标是( )
A. |
B. |
C. |
D. |
某中学进行模拟考试有80个考室,每个考室30个考生,每个考生座位号按1~30号随机编排,每个考场抽取座位号为15号考生试卷评分,这种抽样方法是( )
| A.简单随机抽样 | B.系统抽样 | C.分层抽样 | D.分组抽样 |
执行下边的程序框图,输出的 的值为( )
的值为( )

A. |
B. |
C. |
D. |
函数 (
( )的最小正周期是
)的最小正周期是 ,下面是函数
,下面是函数 对称轴的是( )
对称轴的是( )
A. |
B. |
C. |
D. |
已知数列 为等比数列,若
为等比数列,若 ,则
,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
有5名同学站成一排照相,则甲与乙且甲与丙都相邻的不同排法种数是 ( )
| A.8 | B.12 | C.36 | D.48 |
【改编】已知抛物线 的焦点为
的焦点为 ,过点
,过点 的直线交抛物线于
的直线交抛物线于 两点,
两点, 为坐标原点,则
为坐标原点,则 面积的最小值为( )
面积的最小值为( )
A. |
B. |
C. |
D.由直线的斜率决定 |
某几何体的三视图如图所示,它的体积为( )

A. |
B. |
C. |
D. |
点 、
、 、
、 、
、 在同一球面上,
在同一球面上, 平面
平面 ,
, ,
, ,
, ,则该球的表面积为( )
,则该球的表面积为( )
A. |
B. |
C. |
D. |
已知不等式组 表示平面区域
表示平面区域 ,过区域
,过区域 中的任意一个点
中的任意一个点 ,作圆
,作圆 的两条切线且切点分别为
的两条切线且切点分别为 ,当
,当 最大时,
最大时,  的值为( )
的值为( )
A. |
B. |
C. |
D. |
【原创】已知 ,若
,若 在
在 上恒成立,
上恒成立,
则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知 ,
, ,
, 的夹角为60°,则
的夹角为60°,则 _____.
_____.
【改编】△ 在内角
在内角 的对边分别为
的对边分别为 ,已知
,已知 .若
.若 则边
则边 的最小值为
的最小值为
【改编】双曲线 的左右焦点分别为
的左右焦点分别为 ,过右焦点
,过右焦点 的一条直线交双曲线的左支于点
的一条直线交双曲线的左支于点 ,若
,若 ,且若
,且若 ,则该双曲线的离心率
,则该双曲线的离心率 的取值范围是 .
的取值范围是 .
【原创】已知 (
(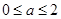 ),若
),若 恒成立,则
恒成立,则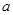 的取值范围为_______.
的取值范围为_______.
已知函数 的部分图象如图所示,
的部分图象如图所示, 是图象的最高点,
是图象的最高点, 为图象与
为图象与 轴的交点,
轴的交点, 为坐标原点,若
为坐标原点,若

(1)求函数 的解析式,
的解析式,
(2)将函数 的图象向右平移2个单位后得到函数
的图象向右平移2个单位后得到函数 的图象,当
的图象,当 时,求函数
时,求函数 的值域.
的值域.
已知四棱锥 的底面是平行四边形,
的底面是平行四边形, 分别是
分别是 的中点,
的中点, ,
, ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求二面角
,求二面角 的余弦值.
的余弦值.
(本小题满分12分)2015年3月15日,中央电视台揭露部分汽车4S店维修黑幕,国家工商总局针对汽车制造行业中的垄断行为加大了调查力度,对汽车零部件加工的相关企业开出了巨额罚单.某品牌汽车制造商为了压缩成本,计划对 、
、 、
、 三种汽车零部件进行招标采购,某著名汽车零部件加工厂参入了该次竞标,已知
三种汽车零部件进行招标采购,某著名汽车零部件加工厂参入了该次竞标,已知 种零部件中标后即可签合同,而
种零部件中标后即可签合同,而 、
、 两种汽车零部件具有很强的关联性,所以公司规定两者都中标才能签合同,否则都不签合同,而三种零部件是否中标互不影响.已知该汽车零部件加工厂中标
两种汽车零部件具有很强的关联性,所以公司规定两者都中标才能签合同,否则都不签合同,而三种零部件是否中标互不影响.已知该汽车零部件加工厂中标 种零部件的概率为
种零部件的概率为 ,只中标
,只中标 种零部件的概率为
种零部件的概率为 ,
, 、
、 两种零部件签订合同的概率为
两种零部件签订合同的概率为 .
.
(Ⅰ)求该汽车零部件加工厂 种汽车零部件中标的概率;
种汽车零部件中标的概率;
(Ⅱ)设该汽车零部件加工厂签订合同的汽车零部件种数为 ,求
,求 的分布列与期望.
的分布列与期望.
(本小题满分12分)已知椭圆 的离心率为
的离心率为 ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线 的焦点重合,过点
的焦点重合,过点 且不垂直于
且不垂直于 轴的直线
轴的直线 与椭圆
与椭圆 相交于
相交于 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)求 的取值范围.
的取值范围.
已知函数 (
( ).
).
(Ⅰ)若函数 在定义域内单调递增,求实数
在定义域内单调递增,求实数 的取值范围;
的取值范围;
(Ⅱ)设 ,
, ,
, (
( )是
)是 图象上的任意两点,若
图象上的任意两点,若 ,使得
,使得 ,求证:
,求证: .
.
选修 :几何证明选讲
:几何证明选讲
如图所示, 是圆
是圆 的切线,
的切线, 为切点,
为切点, 是圆
是圆 的割线,
的割线, 的平分线与
的平分线与 ,
, 分别交于点
分别交于点 ,且
,且 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求 的大小.
的大小.
已知曲线 的极坐标方程是
的极坐标方程是 ,直线
,直线 的参数方程是
的参数方程是 (
( 为参数).
为参数).
(Ⅰ)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)设直线 与
与 轴的交点是
轴的交点是 ,
, 是曲线
是曲线 上一动点,求
上一动点,求 的最大值.
的最大值.
选修4—5: 不等式选讲.
(Ⅰ)设函数 .证明:
.证明: ;
;
(Ⅱ)若实数 满足
满足 ,求证:
,求证: