已知集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知命题 :存在
:存在 ,曲线
,曲线 为双曲线;命题
为双曲线;命题 :
: 的解集是
的解集是 .给出下列结论中正确的有( )
.给出下列结论中正确的有( )
①命题“ 且
且 ”是真命题;
”是真命题;
②命题“ 且(
且(
 )”是真命题;
)”是真命题;
③命题“(
 )或
)或 ”为真命题;
”为真命题;
④命题“(
 )或(
)或(
 )”是真命题.
)”是真命题.
| A.1个 | B.2个 | C.3个 | D.4个 |
设 ,则
,则 =( )
=( )
A. |
B. |
C.5 | D. |
若满足  ,
, 的三角形
的三角形 有两个,则边长
有两个,则边长 的取值范围是 ( )
的取值范围是 ( )
A. |
B. |
C. |
D. |
设数列 的前
的前 项和为
项和为 ,且
,且 ,
, 为常数列,则
为常数列,则 ( )
( )
A. |
B. |
C. |
D. |
点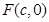 为双曲线
为双曲线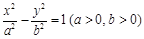 的右焦点,点
的右焦点,点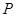 为双曲线左支上一点,线段
为双曲线左支上一点,线段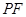 与圆
与圆 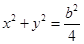 相切于点
相切于点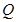 ,且
,且 ,则双曲线的离心率等于( )
,则双曲线的离心率等于( )
A.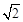 |
B.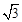 |
C.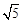 |
D.2 |
设 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 (其中
(其中 )的最大值为3,则
)的最大值为3,则
 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.8 |
已知函数 ,
, .定义:
.定义: ,
, ,……,
,……,
 ,
, …满足
…满足 的点
的点 称为
称为 的
的 阶不动点.则
阶不动点.则 的n
的n
阶不动点的个数是( )
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
设等比数列的首项为 (
( >0),公比为
>0),公比为 (
( ),前
),前 项和为80,其中最大的一项为54,又它的前
项和为80,其中最大的一项为54,又它的前 项和为6560,则
项和为6560,则 ;
; .
.
设函数 .函数
.函数 的最小值为 ;若
的最小值为 ;若 ,使得不等式
,使得不等式 成立,则实数
成立,则实数 的取值范围是 .
的取值范围是 .
已知几何体 的三视图如图所示,其中俯视图和侧视图都是腰长为
的三视图如图所示,其中俯视图和侧视图都是腰长为 的等腰直角三角形,正视图为直角梯形,已知几何体
的等腰直角三角形,正视图为直角梯形,已知几何体 的体积为
的体积为 .则实数
.则实数 的值为 ;将直角三角形
的值为 ;将直角三角形 绕斜边
绕斜边 旋转一周,该旋转体的表面积为 .
旋转一周,该旋转体的表面积为 .


若 ,
,  ,则
,则 ;
; .
.
设函数 为常数),若方程
为常数),若方程 的根都在区间
的根都在区间 内,且函数
内,且函数 在区间
在区间 上单调递增,则实数
上单调递增,则实数 的取值范围是 .
的取值范围是 .
如图,已知 中,
中, ,
, ,
, 是
是 的中点,若向量
的中点,若向量 ,且
,且 的终点
的终点 在
在 的内部(不含边界),则
的内部(不含边界),则 的取值范围是 .
的取值范围是 .

已知函数
 , 若对任意的
, 若对任意的 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .
(本小题满分15分)设函数 ,直线
,直线 与函数
与函数 图象相邻两交点的距离为
图象相邻两交点的距离为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)在 中,角
中,角 所对的边分别是
所对的边分别是 ,若点
,若点 是函数
是函数 图像的一个对称中
图像的一个对称中
心,且 ,求
,求 面积的最大值.
面积的最大值.
(本小题满分15分)设等差数列 的前
的前 项和为
项和为 ,且
,且 ,
, 。
。


(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前
的前 项和为
项和为 ,且
,且 (其中
(其中 是非零的实数),若
是非零的实数),若 ,
, ,
, 成等差数列,问
成等差数列,问 ,
, ,
,  能成等比数列吗?说明理由;
能成等比数列吗?说明理由;
(Ⅲ)设数列 的通项公式
的通项公式 ,是否存在正整数
,是否存在正整数 、
、 (
( ),使得
),使得 ,
, ,
,
成等比数列?若存在,求出所有 、
、 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分15分)如图,在四棱锥 中,
中, 平面
平面 ,
, ,四边形
,四边形 满足
满足 ,
, 且
且 ,点
,点 为
为 中点,点
中点,点 为
为 边上的动点,且
边上的动点,且 .
.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)是否存在实数 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,试求出实数
?若存在,试求出实数 的值;若不存在,
的值;若不存在,
说明理由.
已知椭圆 :
: 的右焦点
的右焦点 ,点
,点 在椭圆
在椭圆 上.
上.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)直线 过点
过点 ,且与椭圆
,且与椭圆 交于
交于 ,
, 两点,过原点
两点,过原点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,如果△
,如果△
的面积为 (
( 为实数),求
为实数),求 的值.
的值.
(本小题满分14分)已知 ,设函数
,设函数 .
.
(Ⅰ)若 在(0, 2)上无极值,求
在(0, 2)上无极值,求 的值;
的值;
(Ⅱ)若存在 ,使得
,使得 是
是 在[0, 2]上的最大值,求实数
在[0, 2]上的最大值,求实数 的取值范围;
的取值范围;
(Ⅲ)若 为自然对数的底数)对任意
为自然对数的底数)对任意 恒成立时
恒成立时 的最大值为1,求实数
的最大值为1,求实数 的
的
取值范围.