“ ”是“
”是“ ”成立的( )
”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分条件 | D.既不充分也不必要条件 |
(原创)设集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
(原创)锐角 满足
满足 ,则
,则 所在范围是( )
所在范围是( )
A. |
B.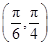 |
C. |
D.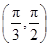 |
已知函数 且
且 有两个零点
有两个零点 、
、 ,则有( )
,则有( )
A. |
B. |
C. |
D. 的范围不确定 的范围不确定 |
已知 ,且
,且 ,成等比数列,则xy( )
,成等比数列,则xy( )
| A.有最大值e | B.有最大值 |
C.有最小值e | D.有最小值 |
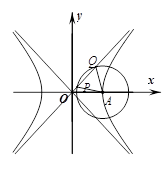
如图,已知双曲线 :
:
 的右顶点为
的右顶点为
 为坐标原点,以
为坐标原点,以 为圆心的圆与双曲线
为圆心的圆与双曲线 的某渐近线交于两点
的某渐近线交于两点 .若
.若 且
且 ,则双曲线
,则双曲线 的离心率为( )
的离心率为( )
A. |
B. |
C. |
D. |
已知 、
、 、
、 是单位圆上互不相同的三个点,且满足
是单位圆上互不相同的三个点,且满足 ,则
,则
的最小值是( )
A. |
B. |
C. |
D. |
已知函数 是定义域为
是定义域为 的偶函数.当
的偶函数.当 时,
时, 若关于
若关于 的方程
的方程 (
( ),有且仅有6个不同实数根,则实数
),有且仅有6个不同实数根,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知数列 则
则 ,数列{an}的通项公式为 .
,数列{an}的通项公式为 .
(原创) 的最大值是 ;当
的最大值是 ;当 取到最大值时
取到最大值时 .
.
某空间几何体的三视图如图所示,则该几何体的体积为 ;表面积为 .

如果实数x,y满足: ,则
,则 的取值范围是 ,
的取值范围是 , 的最大值为 .
的最大值为 .
(原创)已知直线 与圆C:
与圆C: 相交于
相交于 两点,若
两点,若 ,则
,则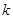 = .
= .
若函数 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围是 .
的取值范围是 .
(原创) 表示不超过
表示不超过 的最大整数,则方程
的最大整数,则方程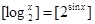 的解集为___________.
的解集为___________.
在 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足
(1)求角 的值;
的值;
(2)若 且
且 ,求
,求 的取值范围.
的取值范围.
(本小题满分15分)已知数列 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中 ,且
,且 成等比数列;数列
成等比数列;数列 的前
的前 项和为
项和为 ,满足
,满足 .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)如果 ,设数列
,设数列 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成立,若存在,求出
成立,若存在,求出 的最小值,若不存在,说明理由.
的最小值,若不存在,说明理由.
如图所示,在边长为12的正方形 中,点
中,点 在线段
在线段 上,且
上,且 ,作
,作 ,分别交
,分别交 于点
于点 ,
, .作
.作 ,分别交
,分别交 于点
于点 ,
, .将该正方形沿
.将该正方形沿 折叠,使得
折叠,使得 与
与 重合,构成如图的三棱柱
重合,构成如图的三棱柱 .
.
(1)求证: 平面
平面 ;
;
(2)求四棱锥 的体积.
的体积.
(原创)已知焦点在 轴上,中心在坐标原点的椭圆C经过点
轴上,中心在坐标原点的椭圆C经过点
(Ⅰ)求椭圆C的短轴长的取值范围;
(Ⅱ)若椭圆C的离心率为 ,且直线
,且直线 分别切椭圆C与圆
分别切椭圆C与圆 (其中
(其中 )于A、B两点,求|AB|的最大值.
)于A、B两点,求|AB|的最大值.
已知函数 定义域是
定义域是 ,且
,且 ,
, ,当
,当 时,
时, .
.
(1)证明: 为奇函数;
为奇函数;
(2)求 在
在 上的表达式;
上的表达式;
(3)是否存在正整数 ,使得
,使得 时,
时, 有解,若存在求出
有解,若存在求出 的值,若不存在说明理由.
的值,若不存在说明理由.