已知全集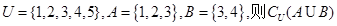 =( ).
=( ).
| A.{3} | B.{5} | C.{1,2,4,5} | D.{1,2,3,4} |
已知等比数列{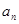 }的前
}的前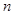 项和为
项和为 ,且
,且 ,则数列
,则数列 的公比
的公比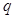 的值为( )
的值为( )
| A.2 | B.3 | C.2或-3 | D.2或3 |
(原创)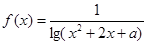 的定义域为
的定义域为 ,则实数
,则实数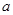 的取值范围是( )
的取值范围是( )
A. |
B.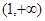 |
C.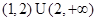 |
D. |
已知平面 ,
,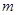 是
是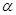 内不同于
内不同于 的直线,那么下列命题中错误的是( )
的直线,那么下列命题中错误的是( )
A.若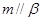 ,则 ,则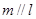 |
B.若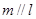 ,则 ,则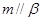 |
C.若 ,则 ,则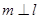 |
D.若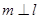 ,则 ,则 |
已知点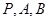 在双曲线
在双曲线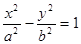 上,直线
上,直线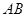 过坐标原点,且直线
过坐标原点,且直线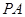 ,
,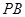 的斜率之积为
的斜率之积为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.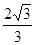 |
B.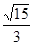 |
C.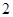 |
D.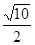 |
(原创)若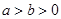 且
且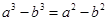 ,则
,则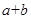 的取值范围是( )
的取值范围是( )
A.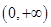 |
B. |
C.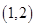 |
D.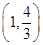 |
(改编)设λ>0,不等式组 所表示的平面区域是W给出下列三个结论:
所表示的平面区域是W给出下列三个结论:
①当λ=1时,W的面积为3;
②∃λ>0,使W是直角三角形区域;
③设点P(x,y),对于∀P∈W有x+ ≤4
≤4
其中,正确的结论有( )
| A.①② | B.①③ | C.②③ | D.①②③ |
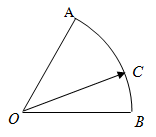
如图,在扇形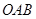 中,
中, ,
,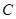 为弧
为弧 上且与
上且与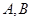 不重合的一个动点,且
不重合的一个动点,且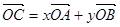 ,若
,若 存在最大值,则
存在最大值,则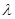 的取值范围为( )
的取值范围为( )
A.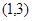 |
B.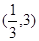 |
C. |
D.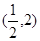 |
(原创)双曲线 (
(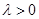 )的离心率是 ;渐近线方程是 .
)的离心率是 ;渐近线方程是 .
.在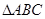 中,
中,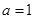 ,
,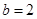 ,
,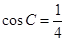 ,则
,则 ;
;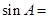
过点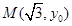 作圆O:
作圆O: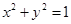 的切线,切点为
的切线,切点为 ,如果
,如果 ,那么切线的斜率是 ;如果
,那么切线的斜率是 ;如果 ,那么
,那么 的取值范围是 .
的取值范围是 .
定义在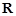 上的奇函数
上的奇函数 满足
满足 ,且在
,且在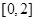 上
上

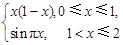 ,则
,则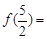 ;若方程
;若方程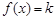 在
在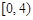 上恰有4个根,则实数
上恰有4个根,则实数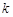 的取值范围是
的取值范围是
(原创)已知等差数列 的前
的前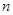 项之和是
项之和是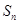 ,若
,若 ,则
,则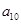 的最小值是___________.
的最小值是___________.
用一个边长为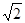 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为1的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为 .
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为1的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为 .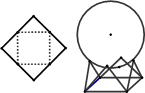
已知函数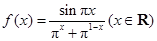 .下列命题:
.下列命题:
①函数 既有最大值又有最小值;
既有最大值又有最小值;
②函数 的图象是轴对称图形;
的图象是轴对称图形;
③函数 在区间
在区间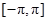 上共有7个零点;
上共有7个零点;
④函数 在区间
在区间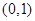 上单调递增.
上单调递增.
其中真命题是 .(填写出所有真命题的序号)
(本小题满分14分)已知函数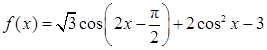
(1)求 的最小正周期和最小值;
的最小正周期和最小值;
(2)若不等式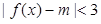 对任意
对任意 恒成立,求实数
恒成立,求实数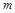 的取值范围
的取值范围
(本小题满分15分)设数列 的前
的前 项和
项和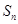 满足
满足 ,其中
,其中
(1)若 ,求
,求 及
及 ;
;
(2)若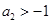 ,求证:
,求证: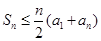 ,并给出等号成立的充要条件
,并给出等号成立的充要条件
如图,四棱锥 的底面是正方形,
的底面是正方形,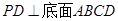 ,点
,点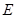 在棱
在棱 上
上
(1)求证:平面 平面
平面 ;
;
(2)当 ,且
,且 时,确定点
时,确定点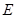 的位置,即求出
的位置,即求出 的值
的值
已知抛物线 的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点
的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点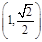
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设点
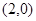 ,过点F2作直线
,过点F2作直线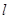 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且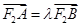 ,若
,若 的取值范围
的取值范围
如果函数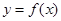 的定义域为
的定义域为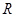 ,对于定义域内的任意
,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”.
性质”.
(1)已知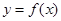 具有“
具有“ 性质”,且当
性质”,且当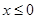 时
时 ,求
,求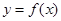 在
在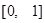 上的最大值.
上的最大值.
(2)设函数 具有“
具有“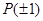 性质”,且当
性质”,且当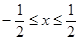 时,
时, .若
.若 与
与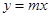 交点个数为2013个,求
交点个数为2013个,求 的值.
的值.