如果质点A按规律 运动,则在
运动,则在 秒的瞬时速度为( )
秒的瞬时速度为( )
| A.6 | B.18 | C.54 | D.81 |
已知函数f(x)=ax2+c,且 =2,则a的值为( )
=2,则a的值为( )
| A.1 | B. |
C.-1 | D.0 |
函数 的导数是( )
的导数是( )
A. |
B. |
C. |
D. |
 =( )
=( )
A.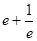 |
B.2e | C.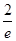 |
D.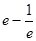 |
抛物线: 的焦点坐标是( )
的焦点坐标是( )
A. |
B. |
C. |
D. |
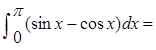 ( )
( )
| A.1 | B.2 | C.0 | D.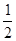 |
如图,函数y=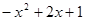 与y=1相交形成一个闭合图形(图中的阴影部分),则该闭合图形的面积是( )
与y=1相交形成一个闭合图形(图中的阴影部分),则该闭合图形的面积是( ) 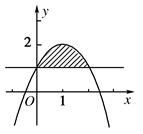
| A.1 | B.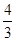 |
C.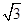 |
D.2 |
对于R上可导的任意函数 ,若满足
,若满足 ,则必有( )
,则必有( )
A. |
B. |
C. |
D. |
曲线 在点
在点 处切线的倾斜角为
处切线的倾斜角为
已知曲线 在点
在点 处的切线与
处的切线与 轴平行,则点
轴平行,则点 的坐标是
的坐标是
若曲线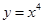 的一条切线
的一条切线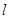 与直线
与直线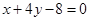 垂直,则
垂直,则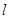 的方程为
的方程为
设 ,若
,若 ,则
,则
设抛物线 上横坐标为6的点到焦点的距离为10,则
上横坐标为6的点到焦点的距离为10,则 . [
. [
曲线 的所有切线中, 斜率最小的切线的方程是 .
的所有切线中, 斜率最小的切线的方程是 .
(本小题满分 分)(1)
分)(1)
(2)
(本小题满分 分)某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x(
分)某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x( ≥10)层,则每平方米的平均建筑费用为560+48
≥10)层,则每平方米的平均建筑费用为560+48 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
(本小题满分 分)
分)
已知 在
在 时有极大值6,在
时有极大值6,在 时有极小值,求
时有极小值,求 的值;并求
的值;并求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.
(本小题满分 分)如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,
分)如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,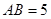 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.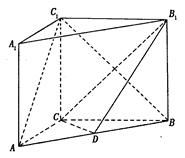
(1)求证:AC⊥BC1;
(2)求多面体 的体积;
的体积;
(3)求二面角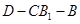 的平面角的正切值.
的平面角的正切值.
(本小题满分 分)如图所示,
分)如图所示, 分别为椭圆
分别为椭圆 的左、右两个焦点,A、B为两个顶点。已知椭圆C上的点
的左、右两个焦点,A、B为两个顶点。已知椭圆C上的点 到
到 两点的距离之和为4。
两点的距离之和为4。
(1)求椭圆C的方程和焦点坐标;
(2)过椭圆C的焦点 作AB的平行线交椭圆于P、Q两点,求弦PQ的长。
作AB的平行线交椭圆于P、Q两点,求弦PQ的长。
已知函数 ,
, 在点
在点 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)若在区间 内,恒有
内,恒有 成立,求
成立,求 的取值范围.
的取值范围.