已知复数
是虚数单位），则
的模为 ．
已知集合
则
．
如图是某市2014年11月份30天的空气污染指数的频率分布直方图．根据国家标准，污染指数在区间
内，空气质量为优；在区间
内，空气质量为良；在区间
内，空气质量为轻微污染；
由此可知该市11月份空气质量为优或良的天数有 天．
执行如图所示的算法流程图，则输出
的值是 ．
已知集合
若从
中各取一个数，则这两个数之和不小于4的概率为 ．
设等差数列
的前
项为
则
的值为 ．
设函数
，则
的值为 ．
已知双曲线
的离心率为2，它的一个焦点是抛物线
的焦点，则双曲线的标准方程为 ．
已知函数
若
则函数
的最小正周期为 ．
在三棱柱
中，侧棱
平面
底面△
是边长为2的正三角形，则此三棱柱的体积为 ．
如图，半径为2的扇形的圆心角为
分别为半径
的中点，
为弧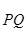
上任意一点，则
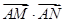的取值范围是 ．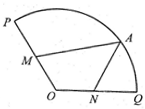
在平面直角坐标系
中，已知圆
点
若圆
上存在点
满足
则实数
的取值范围是 ．
已知实数
满足条件
若不等式
恒成立，则实数
的最大值是 ．
若函数
有三个不同的零点，则实数
的取值范围是 ．
在△
，角
的对边分别为
已知
（1）求
的值；
（2）若
求△的面积．
如图，矩形
所在平面与三角形
所在平面相交于
平面
（1）求证：
平面
（2）若点
在线段
上，
为线段
中点，求证：
平面
如图，在
地正西方向
的
处和正东方向
的
处各一条正北方向的公路
和
现计划在和
路边各修建一个物流中心
和
．为缓解交通压力，决定修建两条互相垂直的公路
和
设
（1）为减少周边区域的影响，试确定
的位置，使△
与△
的面积之和最小；
（2）为节省建设成本，试确定的位置，使
的值最小．
如图，已知椭圆
其率心率为
两条准线之间的距离为
分别为椭圆
的上、下顶点，过点
的直线
分别与椭圆交于
两点．
（1）椭圆的标准方程；
（2）若△
的面积是△
的面积的
倍，求的最大值．
设正项数列
的前
项和为
且
正项等比数列满足：
（1）求数列、
的通项公式；
（2）设
数列
的前项和为
求所有正整数
的值，使得
恰好为数列中的项．
已知函数
其中
为常数．
（1）当
时，若函数
在
上的最小值为
求
的值；
（2）讨论函数在区间
上单调性；
（3）若曲线
上存在一点
使得曲线在点
处的切线与经过点的另一条切线互相垂直，求
的取值范围．
如图，已知直线
为圆
的切线，切点为
点
在圆上，
的角平分线
交圆于点
垂直交圆于点
证明：
已知矩阵
的逆矩阵
，求曲线
在矩阵对应的交换作用下所得的曲线方程．
已知曲线
的参数方程为
为参数），在平面直角坐标系中，以坐标原点为极点，
轴的非负半轴极轴建立极坐标系，曲线
的极坐标方程为
，求与交点的极坐标，其中
已知
都是正数，求证：
如图，在菱形
中，
沿对角线
将△
折起，使
之间的距离为
若
分别为线段
上的动点
（1）求线段
长度的最小值；
（2）当线段长度最小时，求直线与平面
所成角的正弦值
设
且
对于二项式
（1）当
时，分别将该二项式表示为
的形式；
（2）求证：存在
使得等式
与
同时成立．