命题“存在 R,
R,
 0”的否定是( )
0”的否定是( )
A.不存在 R, R,  >0 >0 |
B.存在 R, R,   0 0 |
C.对任意的 R, R,   0 0 |
D.对任意的 R, R,  >0 >0 |
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是 ( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
为得到函数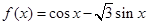 ,只需将函数
,只需将函数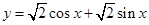 ( )
( )
A.向左平移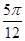 |
B.向右平移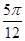 |
C.向左平移 |
D.向右平移 |
已知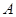 、
、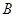 、
、 为直线
为直线 上不同的三点,点
上不同的三点,点 直线
直线 ,实数
,实数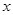 满足关系式
满足关系式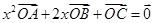 ,有下列结论中正确的个数有 ( )
,有下列结论中正确的个数有 ( )
① 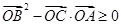 ;
;
② 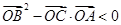 ;
;
③ 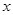 的值有且只有一个;
的值有且只有一个;
④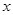 的值有两个;
的值有两个;
⑤ 点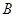 是线段
是线段 的中点.
的中点.
| A.1个 | B.2个 | C.3个 | D.4个 |
已知映射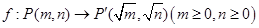 .设点
.设点 ,
,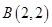 ,点
,点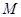 是线段
是线段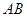 上一动点,
上一动点,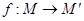 .当点
.当点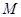 在线段
在线段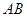 上从点
上从点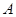 开始运动到点
开始运动到点 结束时,点
结束时,点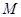 的对应点
的对应点 所经过的路线长度为 ( )
所经过的路线长度为 ( )
A. |
B.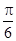 |
C. |
D.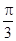 |
如图,已知椭圆C1: +y2=1,双曲线C2:
+y2=1,双曲线C2: —
—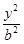 =1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A、B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为 ( )
=1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A、B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为 ( )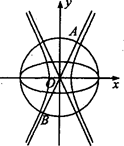
A.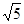 B.5 C.
B.5 C. D.
D.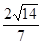
半径为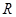 的球内部装有4个半径相同的小球,则小球半径
的球内部装有4个半径相同的小球,则小球半径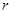 的可能最大值为( ).
的可能最大值为( ).
A.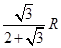 |
B. |
C.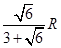 |
D.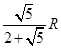 |
某学生对一些对数进行运算,如下图表格所示:
 |
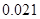 |
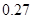 |
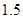 |
 |
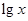 |
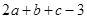 (1) (1) |
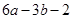 (2) (2) |
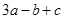 (3) (3) |
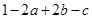 (4) (4) |
 |
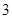 |
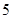 |
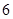 |
 |
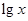 |
 (5) (5) |
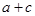 (6) (6) |
 (7) (7) |
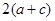 (8) (8) |
 |
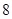 |
 |
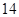 |
|
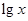 |
 (9) (9) |
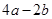 (10) (10) |
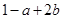 (11) (11) |
|
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是 ( )
A. B.
B.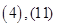 C.
C. D.
D.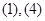
设全集 ,集合
,集合 ,
,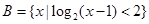 ,则
,则 = ,
= , = ,
= ,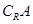 = .
= .
若某多面体的三视图如右图所示,则此多面体的体积为 ,外接球的表面积为 .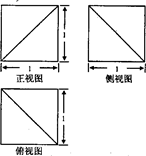
若 表示
表示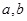 两数中的最大值,若
两数中的最大值,若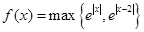 ,则
,则 的最小值为 ,若
的最小值为 ,若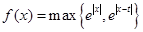 关于
关于 对称,则
对称,则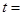 .
.
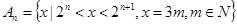 ,若
,若 表示集合
表示集合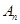 中元素的个数,则
中元素的个数,则 ,则
,则 .
.
直角 的三个顶点都在给定的抛物线
的三个顶点都在给定的抛物线 上,且斜边
上,且斜边 和
和 轴平行,则
轴平行,则 斜边上的高的长度为 .
斜边上的高的长度为 .
圆 的半径为
的半径为 ,
, 为圆周上一点,现将如图放置的边长为
为圆周上一点,现将如图放置的边长为 的正方形(实线所示 ,正方形的顶点
的正方形(实线所示 ,正方形的顶点 和点
和点 重合)沿着圆周顺时针滚动,经过若干次滚动,点
重合)沿着圆周顺时针滚动,经过若干次滚动,点 第一次回到点
第一次回到点 的位置,则点
的位置,则点 走过的路径的长度为 .
走过的路径的长度为 .
已知动点 满足
满足 ,则
,则 的最小值为 .
的最小值为 .
(本小题满分15分)已知 的面积为
的面积为 ,且
,且 .
.
(1)求 ;
;
(2)求 求
求 周长的最大值.
周长的最大值.
(本小题满分15分)在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形, ,
, 侧面
侧面 底面
底面 ,
, ,
, .
.
(1)若 中点为
中点为 .求证:
.求证: ;
;
(2)若 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分15分)函数 ,
,
(1)若 ,试讨论函数
,试讨论函数 的单调性;
的单调性;
(2)若 ,试讨论
,试讨论 的零点的个数;
的零点的个数;
(本小题满分15分)如图,在平面直角坐标系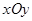 中,离心率为
中,离心率为 的椭圆
的椭圆
 的左顶点为
的左顶点为 ,过原点
,过原点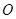 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆 交于
交于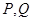 两点,直线
两点,直线 分别与
分别与 轴交于
轴交于 两点.若直线
两点.若直线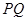 斜率为
斜率为 时,
时, .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)试问以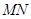 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线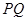 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
(本小题满分14分)已知数列 (
( ,
,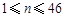 )满足
)满足 ,
,  其中
其中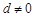 ,
, .
.
(1)当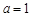 时,求
时,求 关于
关于 的表达式,并求
的表达式,并求 的取值范围;
的取值范围;
(2)设集合 .
.
①若 ,
, ,求证:
,求证: ;
;
②是否存在实数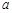 ,
, ,使
,使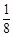 ,
,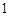 ,
,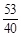 都属于
都属于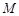 ?若存在,请求出实数
?若存在,请求出实数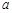 ,
, ;若不存在,请说明理由.
;若不存在,请说明理由.