在 中,“
中,“ ”是“
”是“ 为直角三角形”的( )
为直角三角形”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知数列 满足:
满足: ,且
,且 ,则
,则 的值为( )
的值为( )
| A.7 | B.8 | C.9 | D.10 |
要得到函数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )
A.向右平移 个单位长度 个单位长度 |
B.向左平移 个单位长度 个单位长度 |
C.向右平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
若 是两个相交平面,则在下列命题中,真命题的序号为( )
是两个相交平面,则在下列命题中,真命题的序号为( )
①若直线 ,则在平面
,则在平面 内,一定不存在与直线
内,一定不存在与直线 平行的直线.
平行的直线.
②若直线 ,则在平面
,则在平面 内,一定存在无数条直线与直线
内,一定存在无数条直线与直线 垂直.
垂直.
③若直线 ,则在平面
,则在平面 内,不一定存在与直线
内,不一定存在与直线 垂直的直线.
垂直的直线.
④若直线 ,则在平面
,则在平面 内,一定存在与直线
内,一定存在与直线 垂直的直线.
垂直的直线.
| A.①③ | B.②③ | C.②④ | D.①④ |
已知菱形ABCD的对角线AC长为1,则 =( )
=( )
| A.4 | B.2 | C.1 | D. |
设 , 对于使
, 对于使 成立的所有常数M中,我们把M的最小值1叫做
成立的所有常数M中,我们把M的最小值1叫做 的上确界.若
的上确界.若 ,且
,且 ,则
,则 的上确界为( )
的上确界为( )
A. |
B. |
C. |
D. |
如图,已知椭圆C1: +y2=1,双曲线C2:
+y2=1,双曲线C2: —
— =1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A、B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )
=1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A、B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为( )
A. B.5 C.
B.5 C. D.
D.
如图,正 的中心位于点G
的中心位于点G ,A
,A ,动点P从A点出发沿
,动点P从A点出发沿 的边界按逆时针方向运动,设旋转的角度
的边界按逆时针方向运动,设旋转的角度 ,向量
,向量 在
在 方向的投影为y(O为坐标原点),则y关于x的函数
方向的投影为y(O为坐标原点),则y关于x的函数 的图像是( )
的图像是( )

设全集 ,集合
,集合 ,
, ,则
,则 = ,
= , = ,
= , = .
= .
若变量 满足
满足 ,则
,则 的最大值为 ,
的最大值为 , .
.
已知命题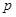 :
: ,
, .命题
.命题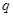 :
: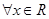 ,
,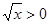 ,则
,则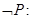 ,命题
,命题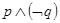 是 (填真命题或假命题)
是 (填真命题或假命题)
若某多面体的三视图如右图所示,则此多面体的体积是 ,此多面体外接球的表面积是 .
已知函数 是奇函数,则
是奇函数,则 .
.
已知点 为圆
为圆 外一点,圆
外一点,圆 上存在点
上存在点 使
使
得 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
已知 是
是 内心,若
内心,若 ,则
,则 = .
= .
已知函数
(1)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(2)设 的内角A、B、C的对边分别为a、b、c,且
的内角A、B、C的对边分别为a、b、c,且 ,
, ,判断△ABC的形状,并求三角形ABC的面积.
,判断△ABC的形状,并求三角形ABC的面积.
已知数列 (
( ,
, )满足
)满足 ,
,  其中
其中 ,
, .
.
(1)当 时,求
时,求 关于
关于 的表达式,并求
的表达式,并求 的取值范围;
的取值范围;
(2)设集合 .若
.若 ,
, ,求证:
,求证: .
.
在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形, ,
, 侧面
侧面 底面
底面 ,
, ,
, .
.
(1)若 中点为
中点为 .求证:
.求证: ;
;
(2)若 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知抛物线 上有四点
上有四点 、
、 ,点M(3,0),直线AB、CD都过点M,且都不垂直于x轴,直线PQ过点M且垂直于x轴,交AC于点P,交BD于点Q.
,点M(3,0),直线AB、CD都过点M,且都不垂直于x轴,直线PQ过点M且垂直于x轴,交AC于点P,交BD于点Q.
(1)求 的值;
的值;
(2)求证: .
.
已知函数 。
。
(1)若 ,求不等式
,求不等式 的解集;
的解集;
(2)若函数 在
在 上有两个零点
上有两个零点 ,求
,求 的取值范围.
的取值范围.