已知集合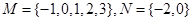 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A.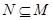 |
B.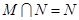 |
C.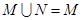 |
D.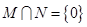 |
下列四个函数中,既是奇函数又是定义域上的单调递增的是 ( )
A.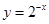 |
B.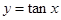 |
C.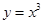 |
D.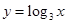 |
已知复数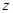 满足
满足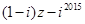
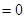 (其中i为虚数单位),则
(其中i为虚数单位),则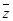 的虚部为 ( )
的虚部为 ( )
A.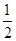 |
B.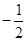 |
C.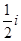 |
D.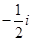 |
数列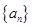 为等差数列,且
为等差数列,且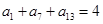 ,则
,则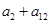 的值为( )
的值为( )
A.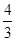 |
B.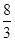 |
C.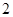 |
D.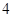 |
设变量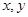 满足约束条件
满足约束条件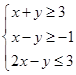 ,则目标函数
,则目标函数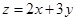 的最小值为 ( )
的最小值为 ( )
| A.6 | B.7 | C.8 | D.23 |
投掷两枚骰子,则点数之和是8的概率为 ( )
A.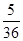 |
B.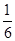 |
C.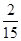 |
D.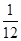 |
在平面直角坐标系中,角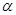 的顶点与原点重合,始边与x轴的非负半轴重合,终边过点
的顶点与原点重合,始边与x轴的非负半轴重合,终边过点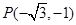 ,则
,则 ( )
( )
A.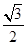 |
B.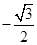 |
C.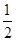 |
D.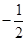 |
某几何体的三视图如图所示,则该几何体的体积为 ( )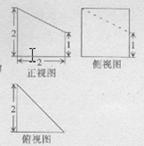
A.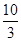 |
B.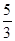 |
C.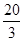 |
D.4 |
执行下方的程序框图,如果输入的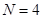 ,那么输出的
,那么输出的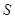 的值为 ( )
的值为 ( )
A.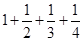 |
B.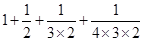 |
C.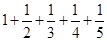 |
D.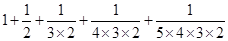 |
在四面体S-ABC中,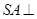 平面
平面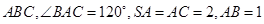 ,则该四面体的外接球的表面积为 ( )
,则该四面体的外接球的表面积为 ( )
A.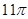 |
B.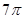 |
C.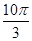 |
D.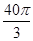 |
已知F是抛物线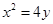 的焦点,直线
的焦点,直线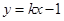 与该抛物线交于第一象限内的点
与该抛物线交于第一象限内的点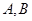 ,若
,若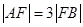 ,则
,则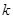 的值是 ( )
的值是 ( )
A.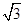 |
B.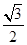 |
C.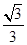 |
D.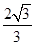 |
已知函数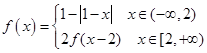 ,设方程
,设方程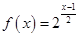 的根从小到大依次为
的根从小到大依次为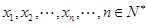 ,则数列
,则数列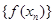 的前n项和为 ( )
的前n项和为 ( )
A.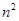 |
B.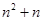 |
C.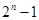 |
D.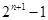 |
已知向量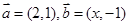 ,且
,且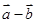 与
与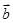 共线,则x的值为
共线,则x的值为
函数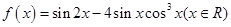 的最小正周期为
的最小正周期为
已知条件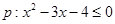 ;条件
;条件 ,若
,若 是
是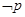 的充分不必要条件,则实数m的取值范围是
的充分不必要条件,则实数m的取值范围是
设点P、Q分别是曲线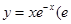 是自然对数的底数)和直线
是自然对数的底数)和直线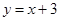 上的动点,则P、Q 两点间距离的最小值为
上的动点,则P、Q 两点间距离的最小值为
(本小题满分12分)在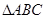 中,角
中,角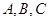 的对边分别为
的对边分别为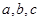 ,且满足
,且满足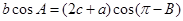
(1)求角B的大小;
(2)若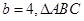 的面积为
的面积为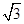 ,求
,求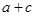 的值.
的值.
(本小题满分12分)4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”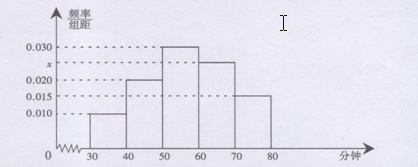
(1)求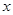 的值并估计全校3000名学生中读书谜大概有多少?(经频率视为频率)
的值并估计全校3000名学生中读书谜大概有多少?(经频率视为频率)
(2)根据已知条件完成下面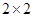 的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?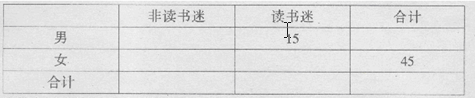
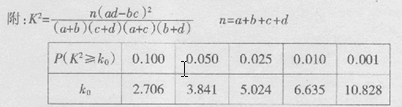
(本小题满分12分)已知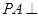 平面
平面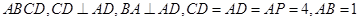 .
.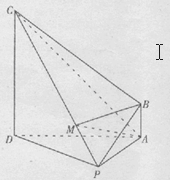
(1)求证: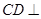 平面
平面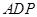 ;
;
(2)M为线段CP上的点,当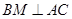 时,求三棱锥
时,求三棱锥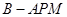 的体积.
的体积.
(本小题满分12分)
已知椭圆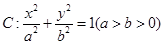 经过点
经过点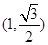 ,离心率为
,离心率为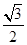 .
.
(1)求椭圆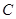 的方程;
的方程;
(2)不垂直与坐标轴的直线 与椭圆
与椭圆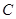 交于
交于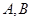 两点, 以
两点, 以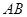 为直径的圆过原点,且线段
为直径的圆过原点,且线段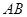 的垂直平分线交y轴于点
的垂直平分线交y轴于点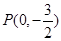 ,求直线
,求直线 的方程。
的方程。
(本小题满分12分)已知函数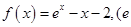 是自然对数的底数
是自然对数的底数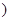 。
。
(1)求函数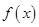 的图象在点
的图象在点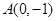 处的切线方程;
处的切线方程;
(2)若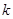 为整数,且当
为整数,且当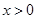 时,
时,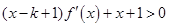 恒成立,其中
恒成立,其中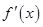 为
为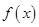 的导函数,求
的导函数,求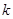 的最大值。
的最大值。
(本小题满分10分)选修4-1:几何证明选讲 如图: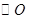 的直径
的直径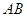 的延长线于弦CD的延长线相交于点P,E为
的延长线于弦CD的延长线相交于点P,E为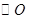 上一点,
上一点,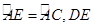 交
交 于点F.
于点F.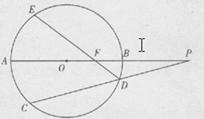
(1)求证: 四点共圆;
四点共圆;
(2)求证: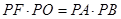 .
.
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系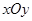 中,直线
中,直线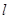 的参数方程
的参数方程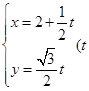 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,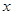 轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为:
轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为: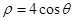 .
.
(1)直线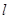 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(2)求直线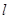 的曲线
的曲线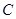 交点的极坐标(
交点的极坐标(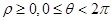 )
)
(本小题满分10分)选修4-5:不等式选讲
设函数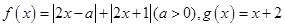 .
.
(1)当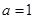 时,求不等式
时,求不等式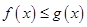 的解集;
的解集;
(2)若 恒成立,求实数
恒成立,求实数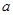 的取值范围.
的取值范围.