若向量
 ,
,
 ,
, ,则实数
,则实数 的值为
的值为
A. |
B. |
C.2 | D.6 |
若集合 ,集合
,集合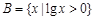 ,则“
,则“ ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知等比数列 的第
的第 项是二项式
项是二项式 展开式的常数项,则
展开式的常数项,则
A. |
B. |
C. |
D. |
若函数 是定义在
是定义在 上的偶函数,则该函数的最大值为
上的偶函数,则该函数的最大值为
| A.5 | B.4 | C.3 | D.2 |
阅读如图所示的程序框图,运行相应的程序.若该程序运行后输出的结果不大于20,则输入
的整数 的最大值为
的最大值为
| A.3 | B.4 | C.5 | D.6 |
已知某市两次数学测试的成绩 和
和 分别服从正态分布
分别服从正态分布 和
和 ,则以下
,则以下
结论正确的是
| A.第一次测试的平均分比第二次测试的平均分要高,也比第二次成绩稳定 |
| B.第一次测试的平均分比第二次测试的平均分要高,但不如第二次成绩稳定 |
| C.第二次测试的平均分比第一次测试的平均分要高,也比第一次成绩稳定 |
| D.第二次测试的平均分比第一次测试的平均分要高,但不如第一次成绩稳定 |
已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,过点
,过点 作直线
作直线 轴交双曲线
轴交双曲线 的渐近线于点
的渐近线于点 .若以
.若以 为直径的圆恰过点
为直径的圆恰过点 ,则该双曲线的离心率为
,则该双曲线的离心率为
A. |
B. |
C.2 | D. |
某单位安排甲、乙、丙三人在某月1日至12日值班,每人4天.
甲说:我在1日和3日都有值班;
乙说:我在8日和9日都有值班;
丙说:我们三人各自值班的日期之和相等.据此可判断丙必定值班的日期是
| A.2日和5日 | B.5日和6日 |
| C.6日和11日 | D.2日和11日 |
若关于 的方程
的方程 有三个实根
有三个实根 ,
, ,
, ,且满足
,且满足 ,则
,则 的最小值为
的最小值为
A. |
B. |
C. |
D.0 |
如图所示为某几何体的正视图和侧视图,则该几何体体积的所有可能取值的集合是 
A. |
B. |
C. |
D. |
复数 (
( 为虚数单位)在复平面上对应的点到原点的距离为__________.
为虚数单位)在复平面上对应的点到原点的距离为__________.
设 是抛掷一枚骰子得到的点数,则方程
是抛掷一枚骰子得到的点数,则方程 有两个不等实根的概率为 .
有两个不等实根的概率为 .
若关于x,y的不等式组  表示的平面区域是一个直角三角形,则k的值为 .
表示的平面区域是一个直角三角形,则k的值为 .
若在圆 上有且仅有两个点到原点
上有且仅有两个点到原点 的距离为1,则实数
的距离为1,则实数 的取值范围是 .
的取值范围是 .
已知面积为 的
的 中,
中, .若点
.若点 为
为 边上的一点,且满足
边上的一点,且满足 ,则当
,则当 取最小时,
取最小时, 的长为 .
的长为 .
(本小题满分13分)将射线 绕着原点逆时针旋转
绕着原点逆时针旋转 后所得的射线经过点
后所得的射线经过点 .
.
(1)求点 的坐标;
的坐标;
(2)若向量 ,
, ,求函数
,求函数 ,
, 的值域.
的值域.
(本小题满分13分)某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛.现有200名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
(1)估算这200名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(2)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得120分,进入最后抢答阶段.抢答规则:抢到的队每次需猜3条谜语,猜对1条得20分,猜错1条扣20分.根据经验,甲队猜对每条谜语的概率均为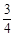 ,乙队猜对前两条的概率均为
,乙队猜对前两条的概率均为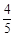 ,猜对第3条的概率为
,猜对第3条的概率为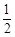 .若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
(本小题满分13分)如图,在四棱柱 中,底面
中,底面 是矩形,且
是矩形,且 ,
, ,
, .若
.若 为
为 的中点,且
的中点,且 .
.
(1)求证: 平面
平面 ;
;
(2)线段 上是否存在一点
上是否存在一点 ,使得二面角
,使得二面角 为
为 ?若存在,求出
?若存在,求出 的长;不存在,说明理由.
的长;不存在,说明理由.
(本小题满分13分)已知点 ,直线
,直线 ,直线
,直线 于
于 ,连结
,连结 ,作线段
,作线段 的垂直平分线交直线
的垂直平分线交直线 于点
于点 .设点
.设点 的轨迹为曲线
的轨迹为曲线 .
.

(1)求曲线 的方程;
的方程;
(2)过点 作曲线
作曲线 的两条切线,切点分别为
的两条切线,切点分别为 ,
,
①求证:直线 过定点;
过定点;
②若 ,过点
,过点 作动直线
作动直线 交曲线
交曲线 于点
于点 ,直线
,直线 交
交 于点
于点 ,试探究
,试探究 是否为定值?若是,求出该定值;不是,说明理由.
是否为定值?若是,求出该定值;不是,说明理由.
(本小题满分14分)已知函数 在点
在点 处的切线斜率为
处的切线斜率为 .
.
(1)求实数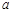 的值;
的值;
(2)设 ,若
,若 对
对 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)已知数列 满足
满足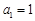 ,
,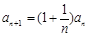 ,
,
求证:当 时
时 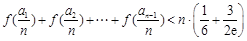
(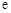 为自然对数的底数,
为自然对数的底数, ).
).
(本小题满分7分)选修4—2:矩阵与变换
在平面直角坐标系中,矩阵 对应的变换将平面上任意一点
对应的变换将平面上任意一点 变换为点
变换为点 .
.
(1)求矩阵 的逆矩阵
的逆矩阵 ;
;
(2)求曲线 在矩阵
在矩阵 的变换作用后得到的曲线
的变换作用后得到的曲线 的方程.
的方程.
(本小题满分7分)选修4-4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点,极轴与 轴的正半轴重合,直线
轴的正半轴重合,直线 的参数方程为
的参数方程为
 (
( 为参数), 圆
为参数), 圆 的极坐标方程为
的极坐标方程为 .
.
(1)求直线 的普通方程和圆
的普通方程和圆 的直角坐标方程;
的直角坐标方程;
(2)若圆 上的点到直线
上的点到直线 的最大距离为
的最大距离为 ,求
,求 的值.
的值.
(本小题满分7分)选修4—5:不等式选讲
已知函数 .
.
(1)求函数 的最小值
的最小值 ;
;
(2)若正实数 满足
满足 ,求证:
,求证: .
.