已知集合 ,
, ,则
,则
A. |
B. |
C. |
D.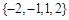 |
若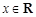 ,则“
,则“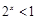 ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人.现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生、本科生与研究生这三类学生中分别抽取
| A.55人,80人,45人 | B.40人,100人,40人 |
| C.60人,60人,60人 | D.50人,100人,30人 |
经过圆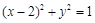 的圆心且与直线
的圆心且与直线 平行的直线方程是
平行的直线方程是
A.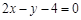 |
B. |
C.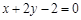 |
D. |
设m,n是两条不同的直线,α,β是两个不同的平面,下列正确的是
A.若m∥α,n α,则m∥n α,则m∥n |
B.若m∥α,m∥β,则α∥β |
| C.若m∥α,α⊥β,则m⊥β | D.若m∥n,m⊥α,则n⊥α |
已知 ,
, ,则
,则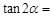
A.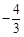 |
B. |
C. |
D.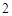 |
下列函数中,既为奇函数又在 内单调递减的是
内单调递减的是
A. |
B.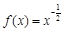 |
C. |
D. |
运行如图所示的程序,若输出 的值为1,则可输入
的值为1,则可输入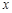 的个数为
的个数为
A. |
B.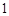 |
C. |
D. |
已知实数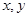 满足
满足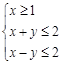 ,若不等式
,若不等式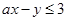 恒成立,则实数
恒成立,则实数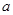 的取值范围为
的取值范围为
A. |
B.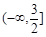 |
C. |
D. |
已知四棱锥 的三视图如图所示,则此四棱锥的侧面积为
的三视图如图所示,则此四棱锥的侧面积为 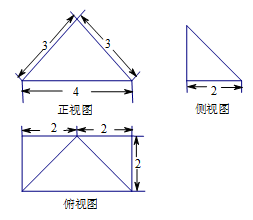
A. |
B. |
C. |
D.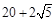 |
已知点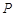 是
是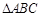 所在平面上一点,
所在平面上一点,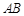 边的中点为
边的中点为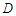 ,若
,若 ,
,
则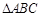 与
与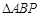 的面积比为
的面积比为
A.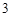 |
B. |
C.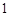 |
D. |
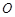 为坐标原点,
为坐标原点, 为曲线
为曲线 上的两个不同点,若
上的两个不同点,若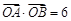 ,则直线
,则直线 与圆
与圆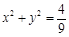 的位置关系是
的位置关系是
| A.相交 | B.相离 | C.相交或相切 | D.相切或相离 |
复数 (
( 为虚数单位),则
为虚数单位),则 .
.
在区间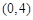 内任取一个实数
内任取一个实数 ,则使不等式
,则使不等式 成立的概率为 .
成立的概率为 .
关于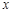 的方程
的方程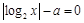 的两个根为
的两个根为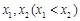 ,则
,则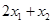 的最小值为 .
的最小值为 .
已知函数 ,且
,且 恒成立.给出下列结论:
恒成立.给出下列结论:
①函数 在
在 上单调递增;
上单调递增;
②将函数 的图象向左平移
的图象向左平移 个单位,所得图象对应的函数为偶函数;
个单位,所得图象对应的函数为偶函数;
③若 ,则函数
,则函数 有且只有一个零点.
有且只有一个零点.
其中正确的结论是 .(写出所有正确结论的序号)
(本小题满分12分)已知等比数列 的前
的前 项和
项和 .
.
(1)求实数 的值和
的值和 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,
, ,求
,求 .
.
(本小题满分12分)某中学刚搬迁到新校区,学校考虑,若非住校生上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课.为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为 ,
, ,
, ,
, ,
, .
.
(1)求频率分布直方图中 的值;
的值;
(2)从统计学的角度说明学校是否需要推迟5分钟上课;
(3)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求恰有一个学生的单程时间落在 上的概率.
上的概率.
(本小题满分12分)已知函数
 在一个周期内的图象如图所示,其中
在一个周期内的图象如图所示,其中
 ,
,
 .
.
(1)求函数 的解析式;
的解析式;
(2)在 中,角
中,角 的对边分别是
的对边分别是 ,且
,且 ,求
,求 的面积.
的面积.
(本小题满分12分)如图四棱锥 中,平面
中,平面 平面
平面 ,
, ,
, ,且
,且 ,
, .
.
(1)求三棱锥 的体积;
的体积;
(2)问:棱 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值,并加以证明;若不存在,请说明理由.
的值,并加以证明;若不存在,请说明理由.
(本小题满分12分)已知点 ,动点
,动点 满足直线
满足直线 与直线
与直线 的斜率之积为
的斜率之积为 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设过点 的直线
的直线 与曲线
与曲线 交于点
交于点 ,记点
,记点 到直线
到直线 的距离为
的距离为 .
.
①求 的值;
的值;
②过点 作直线
作直线 的垂线交直线
的垂线交直线 于点
于点 ,求证:直线
,求证:直线 平分线段
平分线段 .
.
(本小题满分14分)已知函数 (
( ).
).
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若不等式 对任意
对任意 恒成立.
恒成立.
①求实数 的取值范围;
的取值范围;
②试比较 与
与 的大小,并给出证明(
的大小,并给出证明( 为自然对数的底数,
为自然对数的底数, ).
).