复数 等于
等于
A. |
B. |
C. |
D. |
已知全集 ,
, ,
, ,则
,则 等于
等于
A. |
B. |
C. |
D. |
已知 ,则
,则 的值为
的值为
A. |
B. |
C. |
D. |
已知命题 :若
:若 是非零向量,
是非零向量, 是非零实数,则
是非零实数,则 与
与
 方向相反;命题
方向相反;命题 :
: .则下列命题为真命题的是
.则下列命题为真命题的是
A. |
B. |
C. |
D. |
从编号为0,1,2, ,79的80件产品中,采用系统抽样的方法抽取容量为5的一个样本,若编号为42的产品在样本中,则该样本中产品的最小编号为
| A.8 | B.10 | C.12 | D.16 |
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于
| A.28 πcm3 | B.14πcm3 | C.7πcm3 | D.56πcm3 |
函数 ,则下列结论正确的是
,则下列结论正确的是
A.函数 在其定义域内为增函数且是奇函数 在其定义域内为增函数且是奇函数 |
B.函数 在其定义域内为增函数且是偶函数 在其定义域内为增函数且是偶函数 |
C.函数 在其定义域内为减函数且是奇函数 在其定义域内为减函数且是奇函数 |
D.函数 在其定义域内为将函数且是偶函数 在其定义域内为将函数且是偶函数 |
设非空集合 同时满足下列两个条件:
同时满足下列两个条件:
① ;
;
②若 ,则
,则 ,
, .则下列结论正确的是
.则下列结论正确的是
A.若 为奇数,则集合 为奇数,则集合 的个数为 的个数为 |
B.若 为奇数,则集合 为奇数,则集合 的个数为 的个数为 |
C.若 为偶数,则集合 为偶数,则集合 的个数为 的个数为 |
D.若 为偶数,则集合 为偶数,则集合 的个数为 的个数为 |
已知点
 和向量
和向量 =(2,3),若
=(2,3),若 ,则点
,则点 的坐标为 .
的坐标为 .
设随机变量 服从正态分布
服从正态分布 ,若
,若 ,则
,则 .
.
函数 在
在 处取得最小值.
处取得最小值.
已知方程 (
( 是常数)表示曲线
是常数)表示曲线 ,给出下列命题:
,给出下列命题:
①曲线 不可能为圆;
不可能为圆;
②曲线 不可能为抛物线;
不可能为抛物线;
③若曲线 为双曲线,则
为双曲线,则 或
或 ;
;
④若曲线 为焦点在x轴上的椭圆,则
为焦点在x轴上的椭圆,则 .
.
其中真命题的编号为 .
设实数x,y 满足条件 ,若
,若 的最小值为0,则实数
的最小值为0,则实数 的最小值与最大值的和等于 .
的最小值与最大值的和等于 .
(极坐标与参数方程选讲选做题)已知两曲线的参数方程分别为 (
( 为参数)和
为参数)和 (
( 为参数),则它们的交点坐标为 .
为参数),则它们的交点坐标为 .
(几何证明选做题)如图,从圆 外一点
外一点 引圆的切线
引圆的切线 和割线
和割线 ,已知
,已知 ,
, ,圆心
,圆心 到
到 的距离为
的距离为 ,则点
,则点 与圆
与圆 上的点的最短距离为 .
上的点的最短距离为 .
(本小题满分12分)在 中,内角
中,内角 的对边分别为
的对边分别为 已知
已知 ,
, .
.
(1)求 的面积;
的面积;
(2)求
(本小题满分12分)如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为[50,60),[60,70),[70,80),[80,90),[90,100],据此解答如下问题.

(1)求全班人数及分数在[80,100]之间的频率;
(2)现从分数在[80,100]之间的试卷中任取 份分析学生失分情况,设抽取的试卷分数在[90,100]的份数为 X ,求 X 的分布列和数学望期.
份分析学生失分情况,设抽取的试卷分数在[90,100]的份数为 X ,求 X 的分布列和数学望期.
如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, 为
为 与
与 的交点,
的交点,  为
为 上任意一点.
上任意一点.
(1)证明:平面 平面
平面 ;
;
(2)若 平面
平面 ,并且二面角
,并且二面角 的大小为
的大小为 ,求
,求 的值.
的值.
已知数列  中,
中, 
(1)求证:数列  是等比数列;
是等比数列;
(2)若  是数列
是数列  的前n项和,求满足
的前n项和,求满足  的所有正整数n
的所有正整数n
(本小题满分14分)如图,已知椭圆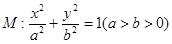 ,焦距为
,焦距为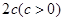 ,其离心率为
,其离心率为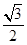 ,
,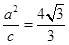 ,
,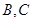 分别为椭圆
分别为椭圆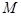 的上、下顶点,过点
的上、下顶点,过点 的直线
的直线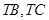 分别交椭圆
分别交椭圆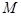 于
于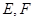 两点.
两点.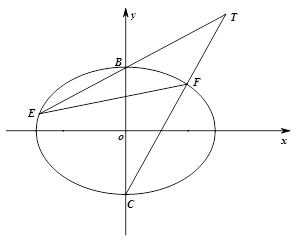
(1)求椭圆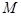 的标准方程;
的标准方程;
(2)若 的面积是
的面积是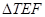 的面积的
的面积的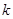 倍,求
倍,求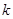 的最大值.
的最大值.
(本小题满分14分)设函数 .
.
(1)若函数 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值;
(2)若存在 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.