已知z为复数,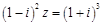 (i为虚数单位),则
(i为虚数单位),则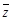 =
=
A.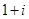 |
B.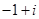 |
C.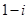 |
D.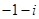 |
已知全集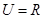 ,
,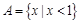 ,
, ,则集合
,则集合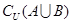 =
=
A. |
B. |
C. |
D.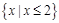 |
一个几何体的三视图如图所示,正视图和侧视图都是等边三角形。若该几何体的四个顶点在空间直角坐标系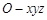 中的坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标可能为
中的坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标可能为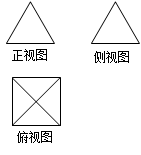
| A.(1,1,1) | B.(1,1,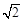 ) ) |
C.(1,1, ) ) |
D.(2,2, ) ) |
、已知随机变量 的分布列是其中
的分布列是其中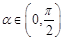 ,则
,则
 |
-1 |
0 |
2 |
| P |
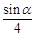 |
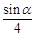 |
 |
A、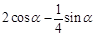 B、
B、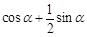 C、0 D、1
C、0 D、1
已知 的二项展开式的奇数项二项式系数和为64,若
的二项展开式的奇数项二项式系数和为64,若
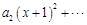
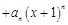 ,则
,则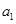 等于
等于
| A.-14 | B.448 | C.-1024 | D.-16 |
若函数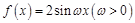 的图象在
的图象在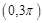 上恰有一个极大值和一个极小值,则
上恰有一个极大值和一个极小值,则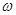 的取值范围是
的取值范围是
A. |
B.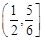 |
C.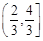 |
D. |
已知有序数对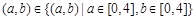 ,则方程
,则方程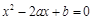 有实根的概率为
有实根的概率为
A.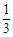 |
B.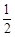 |
C.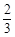 |
D. |
已知实数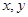 满足
满足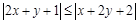 ,且
,且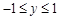 ,则
,则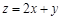 的最大值为
的最大值为
| A.6 | B.5 | C.4 | D.-3 |
如图,直线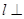 平面
平面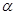 ,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①
,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①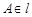 ,②
,②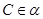 ,则B,O两点间的最大距离为
,则B,O两点间的最大距离为
A.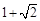 |
B.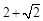 |
C.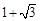 |
D.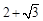 |
已知函数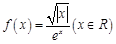 ,若关于
,若关于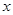 的方程
的方程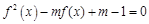 恰好有4个不相等的实数根,则实数
恰好有4个不相等的实数根,则实数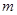 的取值范围为
的取值范围为
A.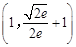 |
B.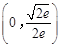 |
C. |
D. |
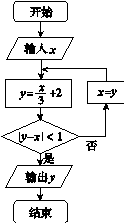
执行如图的程序框图,若输入 ,则输出
,则输出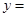 .
.
在等比数列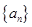 中,对于任意
中,对于任意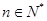 都有
都有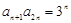 ,则
,则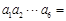 .
.
设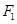 、
、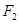 是双曲线
是双曲线 的左、右焦点,
的左、右焦点,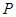 是双曲线右支上一点,满足
是双曲线右支上一点,满足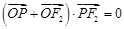 (
( 为坐标原点),且
为坐标原点),且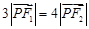 ,则双曲线的离心率为 .
,则双曲线的离心率为 .
数列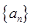 共有12项,其中
共有12项,其中 ,且
,且 ,则满足这种条件的不同数列的个数为 .
,则满足这种条件的不同数列的个数为 .
如图,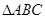 内接于圆
内接于圆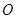 ,直线
,直线 平行
平行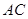 交线段
交线段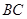 于
于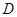 ,交线段
,交线段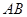 于
于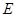 ,交圆
,交圆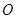 于
于 ,交圆
,交圆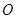 在点
在点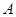 的切线于
的切线于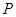 .若
.若 ,
,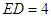 ,
, ,则
,则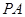 的长为 .
的长为 . 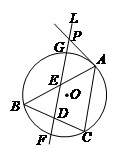
已知曲线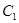 的参数方程为
的参数方程为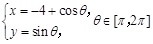 ,若以坐标原点O为极点,
,若以坐标原点O为极点,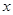 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线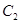 的极坐标方程为
的极坐标方程为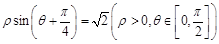 ,那么C1上的点到曲线C2上的点的距离的最小值为 .
,那么C1上的点到曲线C2上的点的距离的最小值为 .
设 ,其中
,其中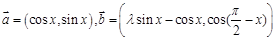 ,
,
已知 满足
满足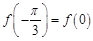
(1)求函数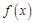 的单调递增区间;
的单调递增区间;
(2)求不等式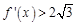 的解集.
的解集.
已知等差数列 满足
满足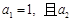 、
、 、
、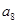 成等比数列,数列
成等比数列,数列 的前
的前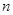 项和
项和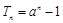 (其中
(其中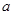 为正常数).
为正常数).
(1)求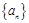 的前项和
的前项和 ;
;
(2)已知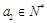 ,
,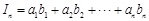 ,求
,求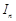
如图,在四棱锥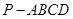 中,
中, 底面
底面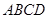 ,底面
,底面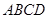 是梯形,其中
是梯形,其中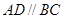 ,
, ,
,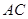 与
与 交于点
交于点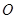 ,
, 是
是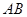 边上的点,且
边上的点,且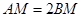 ,已知
,已知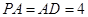 ,
, ,
, .
.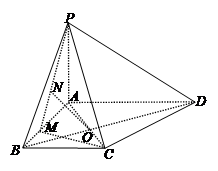
(1)求平面 与平面
与平面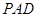 所成锐二面角的正切;
所成锐二面角的正切;
(2)已知 是
是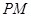 上一点,且
上一点,且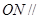 平面
平面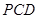 ,求
,求 的值.
的值.
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作.
(1)如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人,再从这8人中选3人,那么至少有一人是甲部门人选的概率是多少?
(2)若从所有甲部门人选中随机选3人,用X表示所选人员中能担任助理工作的人数,写出X的分布列,并求出X的数学期望.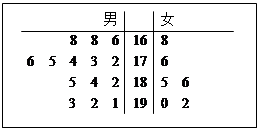
已知椭圆C: 的离心率为
的离心率为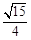 ,
,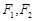 是椭圆的两个焦点,
是椭圆的两个焦点,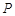 是椭圆上任意一点,且
是椭圆上任意一点,且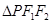 的周长是
的周长是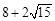 .
.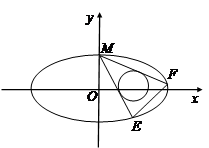
(1)求椭圆C的方程;
(2)设圆T: ,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在
,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在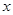 轴上移动且
轴上移动且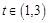 时,求
时,求 的斜率的取值范围.
的斜率的取值范围.
已知函数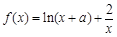 ,
,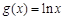 .
.
(1)已知 在
在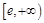 上是单调函数,求
上是单调函数,求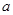 的取值范围;
的取值范围;
(2)已知 满足
满足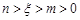 ,且
,且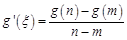 ,试比较
,试比较 与
与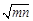 的大小;
的大小;
(3)已知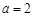 ,是否存在正数
,是否存在正数 ,使得关于
,使得关于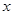 的方程
的方程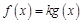 在
在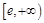 上有两个不相等的实数根?如果存在,求
上有两个不相等的实数根?如果存在,求 满足的条件;如果不存在,说明理由.
满足的条件;如果不存在,说明理由.