已知复数 满足
满足 ,则
,则 的虚部为( )
的虚部为( )
A. |
B. |
C. |
D. |
已知集合 ,则
,则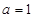 是
是 的( )
的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
设单位向量 的夹角为
的夹角为 ,
, ,则
,则  ( )
( )
A. |
B. |
C. |
D. |
已知等差数列 满足
满足 ,则下列选项错误的是( )
,则下列选项错误的是( )
A. |
B. |
C. |
D. |
双曲线 的顶点到其渐近线的距离为( )
的顶点到其渐近线的距离为( )
A. |
B. |
C. |
D. |
已知 满足约束条件
满足约束条件 ,则
,则 的最大值为( )
的最大值为( )
A. |
B. |
C. |
D. |
周期为4的奇函数 在
在 上的解析式为
上的解析式为 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知 是不同的直线,
是不同的直线, 是不同的平面,以下命题正确的是( )
是不同的平面,以下命题正确的是( )
①若 ∥
∥ ,
, ,则
,则 ∥
∥ ;
;
②若 ,
, ∥
∥ ,则
,则 ;
;
③若 ∥
∥ ,则
,则 ∥
∥ ;
;
④若 ,
, ∥
∥ ,
, ∥
∥ ,则
,则 ;
;
| A.②③ | B.③ | C.②④ | D.③④ |
在 中,内角
中,内角 的对边分别是
的对边分别是 ,若
,若 ,
, 的面积为
的面积为 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
设 为函数
为函数 的导函数,已知
的导函数,已知 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A. 在 在 单调递增 单调递增 |
B. 在 在 单调递减 单调递减 |
C. 在 在 上有极大值 上有极大值 |
D. 在 在 上有极小值 上有极小值 |
用分层抽样的方式对某品牌同一批次两种型号的产品进行抽查,已知样本容量为80,其中有50件甲型号产品,乙型号产品总数为1800,则该批次产品总数为________.
右面的程序框图输出的 的值为_____________.
的值为_____________.
已知 且
且 ,则
,则 的最小值为______.
的最小值为______.
若 , 则
, 则 _________.
_________.
函数 的零点个数为___________.
的零点个数为___________.
(本小题满分12分)已知向量
 ,
,
函数 ,若函数
,若函数 的图象的两个相邻对称中心的距离为
的图象的两个相邻对称中心的距离为 .
.
(Ⅰ)求函数 的单调增区间;
的单调增区间;
(Ⅱ)若将函数 的图象先向左平移
的图象先向左平移 个单位,然后纵坐标不变,横坐标缩短为原来的
个单位,然后纵坐标不变,横坐标缩短为原来的 倍,得到函数
倍,得到函数 的图象,当
的图象,当 时,求函数
时,求函数 的值域.
的值域.
(本小题满分12分)一汽车4S店新进A,B,C三类轿车,每类轿车的数量如下表:
| 类别 |
A |
B |
C |
| 数量 |
4 |
3 |
2 |
同一类轿车完全相同,现准备提取一部分车去参加车展.
(Ⅰ)从店中一次随机提取2辆车,求提取的两辆车为同一类型车的概率;
(Ⅱ)若一次性提取4辆车,其中A,B,C三种型号的车辆数分别记为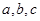 ,记
,记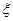 为
为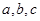 的最大值,求
的最大值,求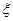 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知  是各项都为正数的数列,其前
是各项都为正数的数列,其前  项和为
项和为  ,且
,且 为
为 与
与 的等差中项.
的等差中项.
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)设 求
求 的前
的前 项和
项和 .
.
(本小题满分12分)如图: 是直径为
是直径为 的半圆,
的半圆, 为圆心,
为圆心, 是
是 上一点,且
上一点,且 .
. ,且
,且 ,
, ,
, 为
为 的中点,
的中点, 为
为 的中点,
的中点, 为
为 上一点,且
上一点,且 .
.
(Ⅰ) 求证: ∥平面
∥平面 ;
;
(Ⅱ)求平面 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.
(本小题满分13分)已知函数
 .
.
(Ⅰ)若 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;
(Ⅱ)若 ,求函数
,求函数 的极小值;
的极小值;
(Ⅲ)若存在实数 使
使 在区间
在区间 且
且 上有两个不同的极值点,求
上有两个不同的极值点,求 的最小值.
的最小值.
(本小题满分14分)如图,过原点 的直线
的直线 分别与
分别与 轴,
轴, 轴成
轴成 的角,点
的角,点 在
在 上运动,点
上运动,点 在
在 上运动,且
上运动,且 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设 是轨迹
是轨迹 上不同两点,且
上不同两点,且 ,
,
(ⅰ)求 的取值范围;
的取值范围;
(ⅱ)判断 的面积是否为定值?若是,求出该定值,不是请说明理由.
的面积是否为定值?若是,求出该定值,不是请说明理由.