已知复数 满足
满足 ,则
,则 的虚部为( )
的虚部为( )
A. |
B. |
C. |
D. |
已知集合 ,则
,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条 |
| C.充要条件 | D.既不充分也不必要条件 |
设单位向量 的夹角为
的夹角为 ,
, ,则
,则  ( )
( )
A. |
B. |
C. |
D. |
已知等差数列 满足
满足 ,则下列选项错误的是( )
,则下列选项错误的是( )
A. |
B. |
C. |
D. |
一几何体的三视图如图所示,则该几何体的体积为( )
A. |
B. |
C. |
D. |
双曲线 的顶点到其渐近线的距离为( )
的顶点到其渐近线的距离为( )
A. |
B. |
C. |
D. |
周期为4的奇函数 在
在 上的解析式为
上的解析式为 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知 满足约束条件
满足约束条件 ,则
,则 的最大值为( )
的最大值为( )
A. |
B. |
C. |
D. |
在 中,内角
中,内角 的对边分别是
的对边分别是 ,若
,若 ,
, 的面积为
的面积为 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
设 为函数
为函数 的导函数,已知
的导函数,已知 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A. 在 在 单调递增 单调递增 |
B. 在 在 单调递减 单调递减 |
C. 在 在 上有极大值 上有极大值 |
D. 在 在 上有极小值 上有极小值 |
右面的程序框图输出的 的值为_____________.
的值为_____________.
在区间 上随机取一个点
上随机取一个点 ,若
,若 满足
满足 的概率为
的概率为 ,则
,则 ____________.
____________.
若点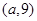 在函数
在函数 的图象上,则
的图象上,则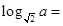 _______.
_______.
已知 且
且 ,则
,则 的最小值为______.
的最小值为______.
函数 的零点个数为___________.
的零点个数为___________.
(本小题满分12分) 已知向量
 ,函数
,函数 ,若函数
,若函数 的图象的两个相邻对称中心的距离为
的图象的两个相邻对称中心的距离为 .
.
(Ⅰ)求函数 的单调增区间;
的单调增区间;
(Ⅱ)将函数 的图象先向左平移
的图象先向左平移 个单位,然后纵坐标不变,横坐标缩短为原来的
个单位,然后纵坐标不变,横坐标缩短为原来的 倍,得到函数
倍,得到函数 的图象,当
的图象,当 时,求函数
时,求函数 的值域.
的值域.
(本小题满分12分)一汽车厂生产A,B,C三类轿车,某月的产量如下表(单位:辆):
| 类别 |
A |
B |
C |
| 数量 |
400 |
600 |
 |
按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(Ⅰ)求 的值;
的值;
(Ⅱ)用分层抽样的方法在A,B类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆A类轿车的概率;
(Ⅲ)用随机抽样的方法从A,B两类轿车中各抽取4辆,进行综合指标评分,经检测它们的得分如图,比较哪类轿车综合评分比较稳定. 
(本小题满分12分)已知  是各项都为正数的数列,其前
是各项都为正数的数列,其前  项和为
项和为  ,且
,且 为
为 与
与 的等差中项.
的等差中项.
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)设 求
求 的前
的前 项和.
项和.
(本小题满分12分)如图: 是直径为
是直径为 的半圆,
的半圆, 为圆心,
为圆心, 是
是 上一点,
上一点,
且 .
. ,且
,且 ,
, ,
, 为
为 的中点,
的中点, 为
为 的中点,
的中点, 为
为 上一点,且
上一点,且 .
.
(Ⅰ)求证: 面 ⊥面
⊥面 ;
;
(Ⅱ)求证: ∥平面
∥平面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
(本小题满分13分)已知函数
 .
.
(Ⅰ)若 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;
(Ⅱ)若 ,求函数
,求函数 的极小值;
的极小值;
(Ⅲ)若方程 在
在 上有两个不等实根,求实数
上有两个不等实根,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆 的离心率
的离心率 ,它的一
,它的一
个顶点在抛物线 的准线上.
的准线上.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设 是椭圆
是椭圆 上两点,已知
上两点,已知 ,且
,且 .
.
(ⅰ)求 的取值范围;
的取值范围;
(ⅱ)判断 的面积是否为定值?若是,求出该定值,不是请说明理由.
的面积是否为定值?若是,求出该定值,不是请说明理由.