已知全集U=R,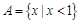 ,
,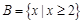 ,则集合
,则集合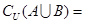 ( )
( )
A.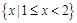 |
B.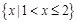 |
C.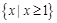 |
D.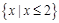 |
已知z为复数, (i为虚数单位),则
(i为虚数单位),则 =
=
A. |
B.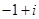 |
C. |
D.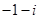 |
一个几何体的三视图如图所示,正视图和侧视图都是等边三角形。若该几何体的四个顶点在空间直角坐标系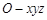 中的坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标可能为
中的坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标可能为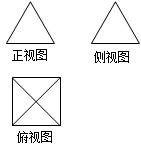
| A.(1,1,1) | B.(1,1,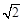 ) ) |
C.(1,1,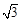 ) ) |
D.(2,2,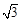 ) ) |
甲、乙两名同学,在班级的演讲比赛中,得分情况如图所示,记甲、乙两人的平均得分分别为 、
、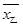 ,则下列判断正确的是
,则下列判断正确的是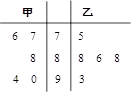
A.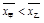 ,甲比乙成绩稳定 ,甲比乙成绩稳定 |
B.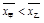 ,乙比甲成绩稳定 ,乙比甲成绩稳定 |
C. ,甲比乙成绩稳定 ,甲比乙成绩稳定 |
D. ,乙比甲成绩稳定 ,乙比甲成绩稳定 |
已知双曲线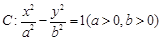 的焦距为
的焦距为 ,抛物线
,抛物线 与双曲线
与双曲线 的渐近线相切,则双曲线
的渐近线相切,则双曲线 的方程为
的方程为
A. |
B.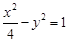 |
C.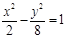 |
D.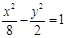 |
已知多项式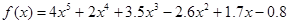 ,用秦九韶算法算
,用秦九韶算法算 时的
时的 值为
值为
| A.22 | B.564.9 | C.20 | D.14130.2 |
数列 为等比数列,其中
为等比数列,其中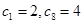 ,
,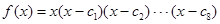 ,
,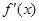 为函数
为函数 的导函数,则
的导函数,则 =
=
A. |
B. |
C. |
D. |
“序数”指每个数字比其左边的数字大的自然数(如1246),在两位的“序数”中任取一个数比36大的概率是
A.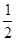 |
B. |
C. |
D.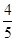 |
已知定义在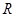 上的奇函数
上的奇函数 ,当
,当 时,
时,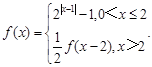 则关于
则关于 的方程
的方程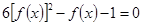 的实数根个数为
的实数根个数为
| A.6 | B.7 | C.8 | D.9 |
若函数 的图象在
的图象在 上恰有一个极大值和一个极小值,则
上恰有一个极大值和一个极小值,则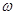 的取值范围是
的取值范围是
A.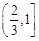 |
B. |
C.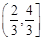 |
D.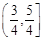 |
执行如图的程序框图,若输入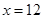 ,则输出
,则输出 .
.
在等比数列 中,对于任意
中,对于任意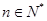 都有
都有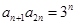 ,则
,则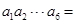 .
.
点 在线性约束条件
在线性约束条件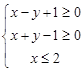 表示的区域内运动,则
表示的区域内运动,则 的最小值为 .
的最小值为 .
若向量 的夹角为45°,且
的夹角为45°,且 ,
, ,则
,则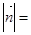 .
.
已知 为实数,则“
为实数,则“ ”是“
”是“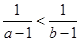 ”的 条件(填“充分不必要”、“必要不充分”及“充要”等).
”的 条件(填“充分不必要”、“必要不充分”及“充要”等).
设 、
、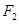 是双曲线
是双曲线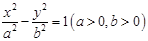 的左、右焦点,若双曲线右支上存在一点
的左、右焦点,若双曲线右支上存在一点 ,使
,使 (
(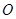 为坐标原点),且
为坐标原点),且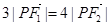 ,则双曲线的离心率为 .
,则双曲线的离心率为 .
已知函数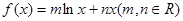 ,曲线
,曲线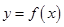 在点
在点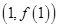 处的切线方程为
处的切线方程为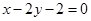 .(1)
.(1)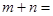 ;(2)若
;(2)若 时,
时,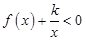 恒成立,则实数
恒成立,则实数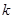 的取值范围是 .
的取值范围是 .
设 ,其中
,其中 ,已知
,已知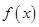 满足
满足
(1)求函数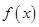 的单调递增区间;
的单调递增区间;
(2)求不等式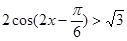 的解集。
的解集。
已知等差数列 满足
满足 、
、 、
、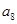 成等比数列,数列
成等比数列,数列 的前
的前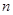 项和
项和 (其中
(其中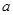 为正常数)
为正常数)
(1)求 的前项和
的前项和 ;
;
(2)已知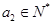 ,
, ,求
,求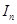
如图,在四棱锥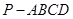 中,
中,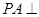 底面
底面 ,底面
,底面 是梯形,其中
是梯形,其中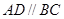 ,
, ,
,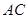 与
与 交于点
交于点 ,
, 是
是 边上的点,且
边上的点,且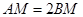 ,已知
,已知 ,
, ,
,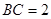 .
.
(1)求平面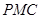 与平面
与平面 所成锐二面角的正切;
所成锐二面角的正切;
(2)已知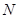 是
是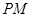 上一点,且
上一点,且 平面
平面 ,求
,求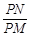 的值.
的值.
若函数 是定义域D内的某个区间
是定义域D内的某个区间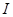 上的增函数,且
上的增函数,且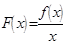 在
在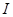 上是减函数,则称
上是减函数,则称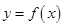 是
是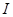 上的“单反减函数”,已知
上的“单反减函数”,已知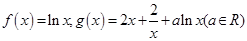
(1)判断 在
在 上是否是“单反减函数”;
上是否是“单反减函数”;
(2)若 是
是 上的“单反减函数”,求实数
上的“单反减函数”,求实数 的取值范围.
的取值范围.
已知椭圆C: 的离心率为
的离心率为 ,
,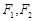 是椭圆的两个焦点,P是椭圆上任意一点,且
是椭圆的两个焦点,P是椭圆上任意一点,且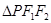 的周长是
的周长是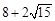
(1)求椭圆C的方程;
(2)设圆T: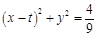 ,过椭圆的上顶点作圆T的两条切线交椭圆于
,过椭圆的上顶点作圆T的两条切线交椭圆于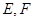 两点,当圆心在
两点,当圆心在 轴上移动且
轴上移动且 时,求
时,求 的斜率的取值范围.
的斜率的取值范围.