设全集 .若集合 , ,则 .
若复数 满足 ,其中 为虚数单位,则 .
若线性方程组的增广矩阵为 、解为 ,则 .
若正三棱柱的所有棱长均为 ,且其体积为 ,则 .
抛物线
( )上的动点
到焦点的距离的最小值为1,则
.
)上的动点
到焦点的距离的最小值为1,则
.
若圆锥的侧面积与过轴的截面面积之比为 ,则其母线与轴的夹角的大小为.
方程 的解为.
在报名的 名男教师和
名男教师和 名女教师中,选取
名女教师中,选取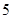 人参加义务献血,要求男、女教师都有,则不同的选取方式的种数为(结果用数值表示).
人参加义务献血,要求男、女教师都有,则不同的选取方式的种数为(结果用数值表示).
已知点 和 的横坐标相同, 的纵坐标是 的纵坐标的2倍, 和 的轨迹分别为双曲线 和 .若 的渐近线方程为 ,则 的渐近线方程为
设 为 , 的反函数,则 的最大值为.
在 的展开式中, 项的系数为(结果用数值表示).
赌博有陷阱.某种赌博每局的规则是:赌客先在标记有1,2,3,4,5的卡片中随机摸取一张,将卡片上的数字作为其赌金(单位:元);随后放回该卡片,再随机摸取两张,将这两张卡片上数字之差的绝对值的1.4倍作为其奖金(单位:元).若随机变量 和 分别表示赌客在一局赌博中的赌金和奖金,则 (元).
已知函数 .若存在 满足 ,且 ( ),则 的最小值为.
在锐角三角形 中, , 为边 上的点, 与 的面积分别为2和4.过 作 于 , 于 ,则 .
设 ,则" 中至少有一个数是虚数"是" 是虚数"的()
| A. | 充分非必要条件 | B. | 必要非充分条件 |
| C. | 充要条件 | D. | 既非充分又非必要条件 |
已知点 的坐标为 ,将 绕坐标原点 逆时针旋转 至 ,则点 的纵坐标为( )
| A. | B. | C. | D. |
记方程①:
,方程②:
,方程③:
,其中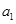 ,
, ,
, 是正实数.当
,
,
成等比数列时,下列选项中,能推出方程③无实根的是()
是正实数.当
,
,
成等比数列时,下列选项中,能推出方程③无实根的是()
| A. | 方程①有实根,且②有实根 | B. | 方程①有实根,且②无实根 |
| C. | 方程①无实根,且②有实根 | D. | 方程①无实根,且②无实根 |
设 是直线 ,与圆 在第一象限的交点,则极限 ()
| A. | B. | C. | D. |
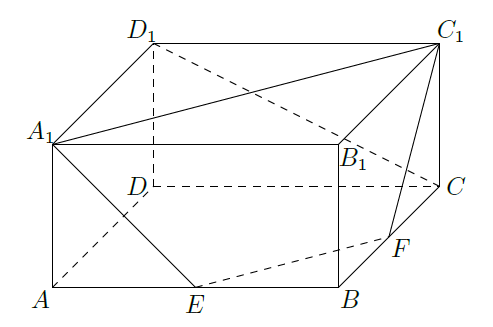
如图,在长方体
中,
,分别是
的中点.证明
四点共面,并求直线
与平面
所成的角的大小.
如图,
三地有直道相通,
千米,
千米,
千米.现甲、乙两警员同时从
地出发匀速前往
地,经过
小时,他们之间的距离为
(单位:千米).甲的路线是
,速度为5千米/小时,乙的路线是
,速度为8千米/小时.乙到达
地后原地等待.设
时乙到达
地.

(1)求
与
的值;
(2)已知警员的对讲机的有效通话距离是3千米.当
时,求
的表达式,并判断
在
上得最大值是否超过3?说明理由.
已知椭圆
,过原点的两条直线
和
分别于椭圆交于
和
,记得到的平行四边形
的面积为
.
(1)设
,用
的坐标表示点
到直线
的距离,并证明
;
(2)设
与
的斜率之积为
,求面积
的值.
已知数列
与
满足
.
(1)若
,且
,求数列
的通项公式;
(2)设
的第
项是最大项,即
,求证:数列
的第
项是最大项;
(3)设
,求
的取值范围,使得
有最大值
与最小值
,且
.
对于定义域为
的函数
,若存在正常数
,使得
是以
为周期的函数,则称
为余弦周期函数,且称
为其余弦周期.已知
是以
为余弦周期的余弦周期函数,其值域为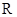 .设
单调递增,
,
.
.设
单调递增,
,
.
(1)验证
是以
为周期的余弦周期函数;
(2)设
.证明对任意
,存在
,使得
;
(3)证明:"
为
在
上得解"的充要条件是"
为方程
在
上有解",并证明对任意
都有
.