不等式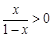 的解集为 .
的解集为 .
若 (
(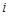 为虚数单位),则实数
为虚数单位),则实数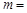 .
.
若函数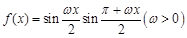 的最小正周期为
的最小正周期为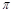 ,则
,则 .
.
集合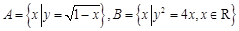 ,则
,则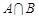 .
.
若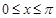 ,则函数
,则函数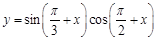 的单调递增区间为 .
的单调递增区间为 .
如图,若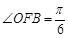 ,
,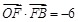 ,则以
,则以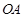 为长半轴,
为长半轴,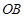 为短半轴,
为短半轴, 为左焦点的椭圆的标准方程为 .
为左焦点的椭圆的标准方程为 .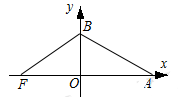
函数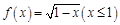 ,若函数
,若函数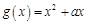 是偶函数,则
是偶函数,则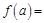 .
.
一个圆锥与一个球的体积相等且圆锥的底面半径是球半径的2倍,若圆锥的高为
1,则球的表面积为 .
已知直线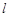 和曲线
和曲线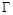 的极坐标方程分别为
的极坐标方程分别为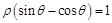 和
和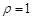 ,若
,若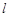 和
和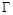 相交于两点
相交于两点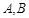 ,则
,则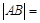 .
.
一个袋子中有7个除颜色外完全相同的小球,其中5个红色,2个黑色.从袋中随机地取出3个小球.其中取到黑球的个数为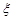 ,则
,则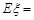 (结果用最简分数作答).
(结果用最简分数作答).
若正方形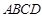 的边长为1,且
的边长为1,且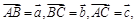 则
则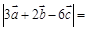 .
.
已知复数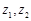 满足
满足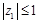 ,
,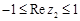 ,
,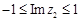 ,若
,若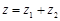 ,则
,则 在复平面上对应的点组成的图形的面积为 .
在复平面上对应的点组成的图形的面积为 .
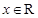 ,用记号
,用记号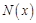 表示不小于实数的最小整数,例如
表示不小于实数的最小整数,例如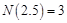 ,
,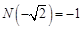 ,
,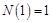 ;则函数
;则函数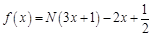 的所有零点之和为 .
的所有零点之和为 .
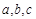 表示直线,
表示直线, 表示平面,下列命题正确的是( )
表示平面,下列命题正确的是( )
A.若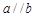 , ,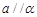 ,则 ,则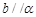 |
B.若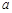 ⊥ ⊥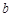 , , 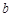 ⊥ ⊥ ,则 ,则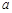 ⊥ ⊥ |
C.若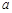 ⊥ ⊥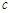 , ,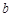 ⊥ ⊥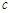 ,则 ,则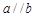 |
D.若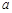 ⊥ ⊥ , ,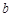 ⊥ ⊥ ,则 ,则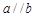 |
”直线与抛物线相切”是“直线与抛物线只有一个公共点”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.非充分非必要条件 |
在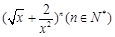 的展开式中,若第五项的系数与第三项的系数之比为56:3,则展开式中的常数项是( )
的展开式中,若第五项的系数与第三项的系数之比为56:3,则展开式中的常数项是( )
| A.第2项 | B.第3项 | C.第4项 | D.第5项 |
已知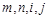 均为正整数,记
均为正整数,记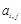 为矩阵
为矩阵 中第
中第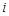 行、第
行、第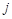 列的元素,且
列的元素,且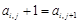 ,
,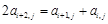 (其中
(其中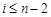 ,
,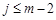 );给出结论:①
);给出结论:①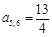 ;②
;②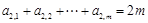 ;③
;③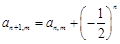 ④若
④若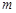 为常数,则
为常数,则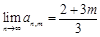 .其中正确的个数是( )
.其中正确的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
已知函数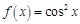 ,
,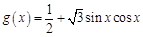 .
.
(1)若直线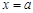 是函数
是函数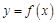 的图像的一条对称轴,求
的图像的一条对称轴,求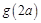 的值;
的值;
(2)若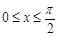 ,求
,求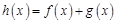 的值域.
的值域.
(本题满分14分,第1小题6分,第2小题8分)
在正方体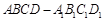 中,
中,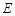 是棱
是棱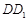 的中点.
的中点.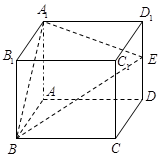
(1)求直线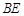 与平面
与平面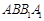 所成角的大小(结果用反三角函数表示)
所成角的大小(结果用反三角函数表示)
(2)在棱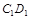 上是否存在一点
上是否存在一点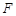 ,使得
,使得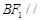 平面
平面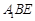 ,若存在,指明点
,若存在,指明点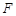 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(本题满分14分,第1小题6分,第2小题8分)
已知函数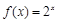 的反函数为
的反函数为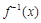
(1)若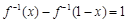 ,求实数
,求实数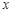 的值;
的值;
(2)若关于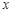 的方程
的方程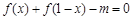 在区间
在区间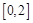 内有解,求实数
内有解,求实数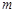 的取值范围;
的取值范围;
(本题满分16分,第1小题4分,第2小题7分,第3小题5分)
如图,射线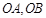 所在的直线的方向向量分别为
所在的直线的方向向量分别为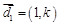 ,
,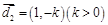 ,点
,点 在
在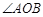 内,
内,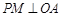 于
于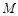 ,
,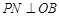 于
于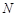 ;
;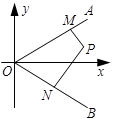
(1)若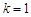 ,
,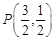 ,求
,求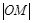 的值;
的值;
(2)若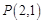 ,
,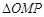 的面积为
的面积为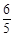 ,求
,求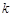 的值;
的值;
(3)已知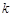 为常数,
为常数,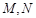 的中点为
的中点为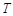 ,且
,且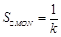 ,当
,当 变化时,求动点
变化时,求动点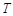 轨迹方程;
轨迹方程;
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列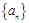 的前
的前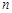 项和为
项和为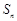 ,且
,且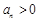 ,
,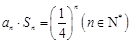
(1)若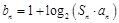 ,求数列
,求数列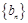 的前
的前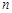 项和
项和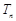 ;
;
(2)若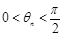 ,
, ,求证:数列
,求证:数列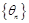 为等比数列,并求出其通项公式;
为等比数列,并求出其通项公式;
(3)记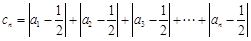 ,若对任意的
,若对任意的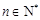 ,
,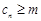 恒成立,求实数
恒成立,求实数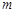 的取值范围.
的取值范围.