已知全集为 ,集合
,集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. 或 或 |
D. 或 或 |
在等差数列 中,
中, ,
, ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D. |
设 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , ,则 ,则 |
设 ,
, 是实数,则“
是实数,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
已知函数 是偶函数,且
是偶函数,且 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知函数 的最小正周期为
的最小正周期为 ,为了得到函数
,为了得到函数 的图象,只要将
的图象,只要将 的图象( )
的图象( )
A.向左平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向右平移 个单位长度 个单位长度 |
设实数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
如图,在正四棱锥 中,
中, ,
, ,
, 分别是
分别是 ,
, ,
, 的中点,动点
的中点,动点 在线段
在线段 上运动时,下列四个结论:①
上运动时,下列四个结论:① ;②
;② ;③
;③ ;④
;④ .中恒成立的为( )
.中恒成立的为( )
| A.①③ | B.③④ | C.①② | D.②③④ |
设 是定义在
是定义在 上的恒不为零的函数,对任意实数
上的恒不为零的函数,对任意实数 ,
, ,都有
,都有 ,若
,若 ,
, ,则数列
,则数列 的前
的前 项和
项和 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知函数
 ,
,
 ,则函数
,则函数 的所有零点之和是( )
的所有零点之和是( )
A. |
B. |
C. |
D. |
函数 的定义域为 .
的定义域为 .
已知 ,
, ,则
,则 .
.
已知某几何体的三视图如图所示, 则该几何体的体积为 . 
已知偶函数 的图象关于直线
的图象关于直线 对称,且
对称,且 时,
时, ,则
,则 .
.
设 ,
, ,…,
,…, ,…是按先后顺序排列的一列向量,若
,…是按先后顺序排列的一列向量,若 ,且
,且 ,则其中模最小的一个向量的序号
,则其中模最小的一个向量的序号 ______.
______.
设 ,
, ,关于
,关于 的方程
的方程 的四个实根构成以
的四个实根构成以 为公比的等比数列,若
为公比的等比数列,若 ,则
,则 的取值范围是 .
的取值范围是 .
已知正四棱锥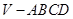 可绕着
可绕着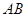 任意旋转,
任意旋转, 平面
平面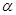 ,若
,若 ,
, ,则正四棱锥
,则正四棱锥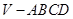 在面
在面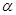 内的投影面积的取值范围是________.
内的投影面积的取值范围是________.
锐角 的内角
的内角 ,
, ,
, ,的对边分别为
,的对边分别为 ,
, ,
, ,已知
,已知
(1)求 的值;
的值;
(2)若 ,
, ,求
,求 的面积.
的面积.
如图所示,正方形 所在的平面与等腰
所在的平面与等腰 所在的平面互相垂直,其中顶
所在的平面互相垂直,其中顶 ,
, ,
, 为线段
为线段 的中点.
的中点.
(1)若 是线段
是线段 上的中点,求证:
上的中点,求证: 平面
平面 ;
;
(2)若 是线段
是线段 上的一个动点,设直线
上的一个动点,设直线 与平面
与平面 所成角的大小为
所成角的大小为 ,求
,求 的最大值.
的最大值.
已知数列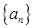 的前
的前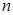 项和
项和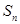 满足
满足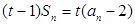 ,(
,(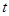 为常数,
为常数,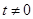 且
且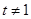 ).
).
(1)求数列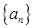 的通项公式;
的通项公式;
(2)设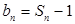 ,且数列
,且数列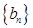 为等比数列.
为等比数列.
①求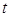 的值;
的值;
②若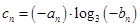 ,求数列
,求数列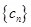 的前
的前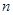 和
和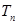 .
.
设向量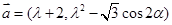 ,
,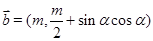 ,其中
,其中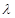 ,
,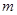 ,
,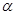 为实数.
为实数.
(1)若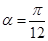 ,且
,且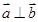 , 求
, 求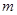 的取值范围;
的取值范围;
(2)若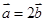 ,求
,求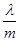 的取值范围.
的取值范围.
已知函数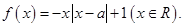
(1)当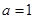 时,求使
时,求使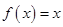 成立的
成立的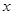 的值;
的值;
(2)当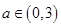 ,求函数
,求函数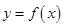 在
在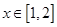 上的最大值;
上的最大值;
(3)对于给定的正数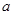 ,有一个最大的正数
,有一个最大的正数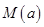 ,使
,使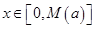 时,都有
时,都有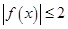 ,试求出这个正数
,试求出这个正数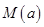 ,并求它的取值范围.
,并求它的取值范围.