已知集合 ,
, ,
, ,则
,则
A. |
B. |
C. |
D. |
已知 ,
, 都是非零实数,则“
都是非零实数,则“ ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
为得到函数 的图象,只要把函数
的图象,只要把函数 图象上所有的点
图象上所有的点
A.横坐标伸长到原来的 倍,纵坐标不变 倍,纵坐标不变 |
B.横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
C.纵坐标伸长到原来的 倍,横坐标不变 倍,横坐标不变 |
D.纵坐标缩短到原来的 倍,横坐标不变 倍,横坐标不变 |
等比数列 的前
的前 项和为
项和为 ,已知
,已知 ,且
,且 ,则实数
,则实数 的值为
的值为
A. |
B. |
C. |
D. |
已知实数 ,
, 满足
满足 则
则 的最小值为
的最小值为
A. |
B. |
C. |
D. |
已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, ,过
,过 作平行于
作平行于 的渐近线的直线交
的渐近线的直线交 于点
于点 .若
.若 ,则
,则 的离心率为
的离心率为
A. |
B. |
C. |
D. |
在四棱柱 中,
中, 平面
平面 ,底面
,底面 是边长为
是边长为 的正方形,侧棱
的正方形,侧棱 的长为
的长为 ,
, 为侧棱
为侧棱 上的动点(包括端点),则
上的动点(包括端点),则
A.对任意的 , , ,存在点 ,存在点 ,使得 ,使得 |
B.当且仅当 时,存在点 时,存在点 ,使得 ,使得 |
C.当且仅当 时,存在点 时,存在点 ,使得 ,使得 |
D.当且仅当 时,存在点 时,存在点 ,使得 ,使得 |
已知向量 ,
, ,定义:
,定义: ,其中
,其中 .若
.若 ,则
,则 的最大值为
的最大值为
A. |
B. |
C. |
D. |
已知函数 为
为 上的偶函数,当
上的偶函数,当 时,
时, ,则
,则 ,
, .
.
已知某几何体的三视图如图所示,这该几何体的体积为 ,表面积为 .
直线 :
: 与圆
与圆 相切.则直线
相切.则直线 的斜率为 ,实数
的斜率为 ,实数 的值为
的值为
已知 ,
, 为锐角,
为锐角, ,
, ,则
,则 ,
, .
.
已知 ,
, ,则
,则 的最小值为 .
的最小值为 .
设等差数列 的前
的前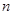 项和为
项和为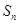 ,公差为正整数
,公差为正整数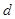 .若
.若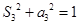 ,则
,则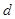 的值为 .
的值为 .
设关于 的方程
的方程 和
和 的实根分别为
的实根分别为 和
和 .若
.若 ,则实数
,则实数 的取值范围为 .
的取值范围为 .
在△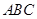 中,角
中,角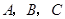 所对的边分别为
所对的边分别为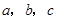 .已知
.已知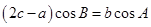 .
.
(Ⅰ)求角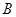 的大小;
的大小;
(Ⅱ)若 ,且△
,且△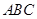 的面积为
的面积为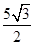 ,求边
,求边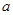 的长.
的长.
已知数列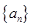 满足:
满足: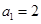 ,
,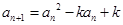 ,(
,(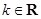 ),
),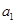 ,
,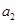 ,
,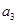 分别是公差不为零的等差数列
分别是公差不为零的等差数列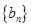 的前三项.
的前三项.
(Ⅰ)求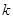 的值;
的值;
(Ⅱ)求证:对任意的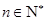 ,
,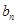 ,
,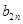 ,
,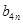 不可能成等比数列.
不可能成等比数列.
如图,在三棱锥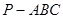 中,△
中,△ 是边长为
是边长为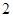 的正三角形,
的正三角形,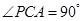 ,
, 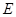 ,
,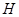 分别为
分别为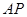 ,
,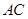 的中点,
的中点,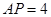 ,
,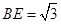 .
. 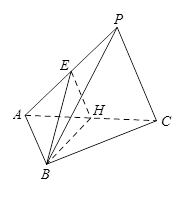
(Ⅰ)求证: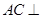 平面
平面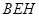 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知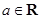 ,函数
,函数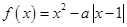 .
.
(Ⅰ)当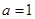 时,求函数
时,求函数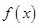 的最小值;
的最小值;
(Ⅱ)当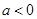 时,讨论
时,讨论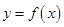 的图象与
的图象与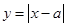 的图象的公共点个数.
的图象的公共点个数.
抛物线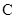 :
: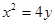 ,直线
,直线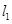 :
: 交
交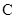 于点
于点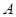 ,交准线于点
,交准线于点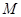 .过点
.过点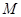 的直线
的直线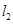 与抛物线
与抛物线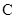 有唯一的公共点
有唯一的公共点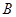 (
(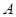 ,
,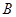 在对称轴的两侧),且与
在对称轴的两侧),且与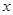 轴交于点
轴交于点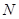 .
.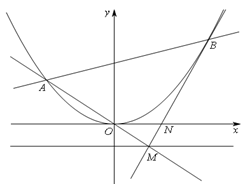
(Ⅰ)求抛物线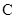 的准线方程;
的准线方程;
(Ⅱ)求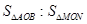 的取值范围.
的取值范围.