下列函数中,在区间 上为增函数的是( )
上为增函数的是( )
A. |
B. |
C. |
D. |
设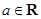 ,则“
,则“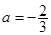 ”是“直线
”是“直线 与直线
与直线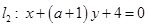 垂直”的( )
垂直”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
将一个长方体截掉一个小长方体,所得几何体的俯视图与侧视图如右图所示,则该几何体的正视图为 ( )

将函数 )的图象向右平移
)的图象向右平移 个单位,再将图象上每一点的横坐标缩短到原来的
个单位,再将图象上每一点的横坐标缩短到原来的 倍(纵坐标不变),所得图象关于直线
倍(纵坐标不变),所得图象关于直线 对称,则
对称,则 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
设不等式组 所表示的平面区域是
所表示的平面区域是 ,平面区域
,平面区域 与
与 关于直线
关于直线 对称,对于
对称,对于 中的任意一点
中的任意一点 与
与 中的任意一点
中的任意一点 的最小值等于( )
的最小值等于( )
| A.2 | B.4 | C. |
D. |
若等差数列 满足
满足 ,则
,则 的最大值为( )
的最大值为( )
A. |
B.3 | C. |
D. |
在平面直角坐标系 中,已知点
中,已知点 是半圆
是半圆 上的一个动点,点
上的一个动点,点 在线段
在线段 的延长线上;当
的延长线上;当 时,点
时,点 的轨迹为( )
的轨迹为( )
| A.线段 | B.圆弧 | C.抛物线一段 | D.椭圆一部分 |
已知集合 ,全集
,全集 ,则
,则 = ,
= ,
若角 终边所在的直线经过
终边所在的直线经过 ,
, 为坐标原点,则
为坐标原点,则 ,
,
已知 则
则 ;当
;当 时,
时, .
.
已知实数 满足
满足 ,则直线
,则直线 恒过定点 ,该直线被圆
恒过定点 ,该直线被圆 所截得弦长的取值范围为 .
所截得弦长的取值范围为 .
已知点 于点
于点 为坐标原点,则
为坐标原点,则 .
.
若对任意 ,直线
,直线 与圆
与圆 均无公共点,则实数m的取值范围是 .
均无公共点,则实数m的取值范围是 .
已知函数 ,
,
(Ⅰ)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)设在 中,内角
中,内角 所对边的边长分别为
所对边的边长分别为 ,且
,且 ,
, ,
,
若 ,求
,求 的值。
的值。
设数列 是公比小于1的正项等比数列,
是公比小于1的正项等比数列, 为数列
为数列 的前
的前 项和,已知
项和,已知 ,
,
且 成等差数列。
成等差数列。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ,且数列
,且数列 是单调递减数列,求实数
是单调递减数列,求实数 的取值范围。
的取值范围。
如图,正四棱锥 中,
中, 分别为
分别为 的中点。设
的中点。设 为线段
为线段 上任意一点。
上任意一点。
(Ⅰ)求证: ;
;
(Ⅱ)当 为线段
为线段 的中点时,求直线
的中点时,求直线 与平面
与平面 所成角的余弦值。
所成角的余弦值。
如图,已知 为抛物线
为抛物线 的焦点,点
的焦点,点 在该抛物线上,其中
在该抛物线上,其中 关于
关于 轴对称(
轴对称( 在第一象限),且直线
在第一象限),且直线 经过点
经过点 .
.
(Ⅰ)若 的重心为
的重心为 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)设 ,其中
,其中 为坐标原点,求
为坐标原点,求 的最小值.
的最小值.
设函数
(Ⅰ)当 时,讨论函数f(x)的零点个数;
时,讨论函数f(x)的零点个数;
(Ⅱ)若对于给定的实数 ,存在实数
,存在实数 ,对于任意实数
,对于任意实数 ,都有不等式
,都有不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。