若 ,则“
,则“ 成立”是“
成立”是“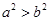 成立”的
成立”的
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分又非必要条件 |
已知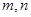 为不同的直线,
为不同的直线, 为不同的平面,则下列说法正确的是
为不同的平面,则下列说法正确的是
A.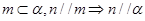 |
B. |
C. |
D. |
设函数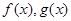 的定义域为
的定义域为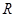 ,且
,且 是奇函数,
是奇函数,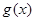 是偶函数,设
是偶函数,设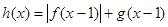 ,则下列结论中正确的是
,则下列结论中正确的是
A. 关于 关于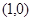 对称 对称 |
B. 关于 关于 对称 对称 |
C. 关于 关于 对称 对称 |
D. 关于 关于 对称 对称 |
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是
| A.2 | B.4 | C.6 | D.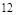 |
已知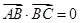 ,
,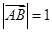 ,
,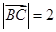 ,
,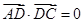 ,则
,则 的最大值为
的最大值为
A.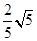 |
B.2 | C.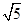 |
D.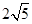 |
若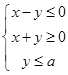 ,若
,若 的最大值为
的最大值为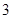 ,则
,则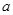 的值是
的值是
A.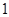 |
B. |
C.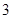 |
D. |
已知双曲线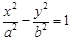 的左、右焦点分别为
的左、右焦点分别为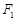 、
、 ,过
,过 作圆
作圆 的切线分别交双曲线的左、右两支于点
的切线分别交双曲线的左、右两支于点 、
、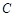 ,且
,且 ,则双曲线的离心率为
,则双曲线的离心率为
A.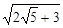 |
B.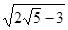 |
C.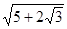 |
D.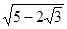 |
已知定义在 上的函数
上的函数 满足:
满足:
① ;
;
② ;
;
③当 时,
时,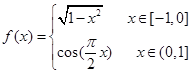 ;
;
则函数 在区间
在区间 上的零点个数为
上的零点个数为
| A.5 | B.6 | C.7 | D.8 |
设全集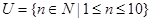 ,
, ,
,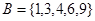 ,则
,则 ,
,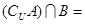 .
.
已知数列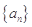 满足
满足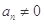 ,
,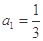 ,
, ,则
,则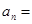 ,
, .
.
已知函数 则
则 ,不等式
,不等式 的解集为 .
的解集为 .
如图,在平面四边形 中,
中, , 则
, 则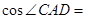 ;又若
;又若 ,则
,则 .
.
如图,在棱长为1的正四面体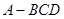 中,平面
中,平面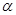 与棱
与棱 分别交于点
分别交于点 ,则四边形
,则四边形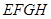 周长的最小值为 .
周长的最小值为 .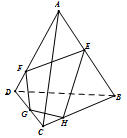
已知 满足
满足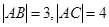 ,
, 是
是 的外心,且
的外心,且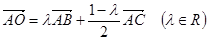 ,则
,则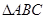 的面积是 .
的面积是 .
如图,某商业中心 有通往正东方向和北偏东
有通往正东方向和北偏东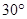 方向的两条街道,某公园
方向的两条街道,某公园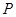 位于商业中心北偏东
位于商业中心北偏东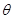 角
角 ,且与商业中心
,且与商业中心 的距离为
的距离为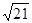 公里处,现要经过公园
公里处,现要经过公园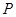 修一条直路分别与两条街道交汇于
修一条直路分别与两条街道交汇于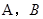 两处,当商业中心
两处,当商业中心 到
到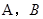 两处的距离之和最小时,
两处的距离之和最小时, 的距离为 公里.
的距离为 公里.
(本小题满分15分)已知点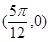 是函数
是函数 图象的一个对称中心.
图象的一个对称中心.
(Ⅰ)求实数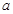 的值;
的值;
(Ⅱ)求 在闭区间
在闭区间 上的最大值和最小值及取到最值时的对应
上的最大值和最小值及取到最值时的对应 值.
值.
(本小题满分15分)已知四边形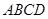 中,
中,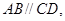
 ,
, 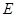 为
为 中点,连接
中点,连接 ,将
,将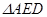 沿
沿 翻折到
翻折到 ,使得二面角
,使得二面角 的平面角的大小为
的平面角的大小为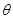 .
.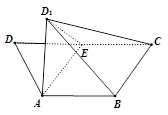
(Ⅰ)证明: ;
;
(Ⅱ)已知二面角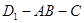 的平面角的余弦值为
的平面角的余弦值为 ,求
,求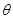 的大小及
的大小及 的长.
的长.
(本小题满分15分)已知椭圆C: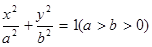 的离心率为
的离心率为 ,左、右焦点分别为
,左、右焦点分别为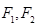 ,点
,点 在椭圆C上,且
在椭圆C上,且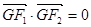 ,
, 的面积为
的面积为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)直线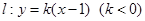 与椭圆
与椭圆 相交于
相交于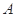 ,
,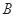 两点.点
两点.点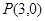 ,记直线
,记直线 的斜率分别为
的斜率分别为 ,当
,当 最大时,求直线
最大时,求直线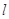 的方程.
的方程.
(本小题满分15分)已知数列 中,
中, (实数
(实数 为常数),
为常数),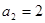 ,
,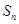 是其前
是其前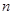 项和,且
项和,且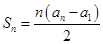 .数列
.数列 是等比数列,
是等比数列, ,
,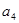 恰为
恰为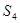 与
与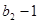 的等比中项.
的等比中项.
(Ⅰ)证明:数列 是等差数列;
是等差数列;
(Ⅱ)求数列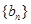 的通项公式;
的通项公式;
(Ⅲ)若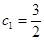 ,当
,当 时
时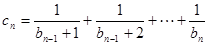 ,
,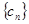 的前
的前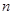 项和为
项和为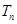 ,求证:对任意
,求证:对任意 ,都有
,都有 .
.
(本小题满分14分)已知函数 ,
,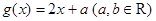 ,且函数
,且函数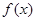 与
与 的图象至多有一个公共点。
的图象至多有一个公共点。
(Ⅰ)证明:当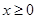 时,
时, ;
;
(Ⅱ)若不等式 对题设条件中的
对题设条件中的 总成立,求
总成立,求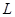 的最小值.
的最小值.
已知复数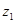 的实部为
的实部为 ,复数
,复数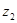 的虚部为
的虚部为 ,且
,且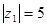 ,
, 是实数,求复数
是实数,求复数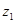 和
和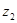 .
.
已知函数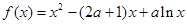 ,求函数
,求函数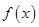 在区间
在区间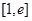 上的最小值.
上的最小值.
求 的展开式中的常数项,其中
的展开式中的常数项,其中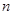 是
是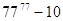 除以
除以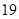 的余数.
的余数.
现有甲类产品有4件,乙类产品有3件,丙类产品有2件,将这些产品随机排成一列,则同类产品不相邻的排法有几种?