函数 的定义域为 .
的定义域为 .
已知全集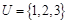 ,集合
,集合 ,集合
,集合 ,则
,则 .
.
函数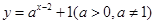 不论
不论 为何值时,其图像恒过的定点为 .
为何值时,其图像恒过的定点为 .
已知幂函数 的图像过点
的图像过点 ,则
,则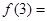 .
.
已知函数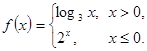 则
则 的值为
的值为
已知 ,若
,若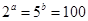 ,则
,则 .
.
关于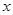 的方程
的方程 的两根为
的两根为 ,且满足
,且满足 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
已知 是有序数对集合
是有序数对集合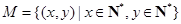 上的一个映射,正整数数对
上的一个映射,正整数数对 在映射
在映射 下对应的为实数
下对应的为实数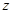 ,记作
,记作 . 对于任意的正整数
. 对于任意的正整数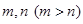 ,映射
,映射 由下表给出:
由下表给出:
则使不等式 的解集为 .
的解集为 .
已知函数 存在唯一零点
存在唯一零点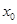 ,则大于
,则大于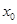 的最小整数为 .
的最小整数为 .
函数 的值域为 .
的值域为 .
生活中常用的十二进位制,如一年有12个月,时针转一周为12个小时,等等,就是逢12进1的计算制,现采用数字0~9和字母A、B共12个计数符号,这些符号与十进制的数的对应关系如下表:
| 十二进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
| 十进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
例如用十二进位制表示A+B=19,照此算法在十二进位制中运算A×B= .
已知函数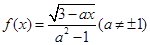 在区间
在区间 上是减函数,则
上是减函数,则 的取值范围是 .
的取值范围是 .
已知大于1的任意一个自然数的三次幂都可表示成连续奇数的和.如:
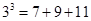

若 是自然数,把
是自然数,把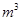 按上述表示,等式右侧的奇数中含有2015,则
按上述表示,等式右侧的奇数中含有2015,则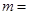 .
.
已知定义在 上的函数
上的函数 既是奇函数,又是周期函数,且周期为
既是奇函数,又是周期函数,且周期为 .当
.当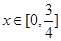 时,
时,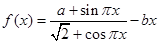 (
( 、
、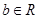 ),则
),则 的值为 .
的值为 .
已知命题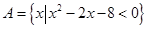 ,
,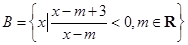 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 ,求
,求 的取值范围.
的取值范围.
已知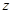 为复数,
为复数, 为实数,且
为实数,且 为纯虚数,其中i是虚数单位.
为纯虚数,其中i是虚数单位.
(1)求复数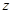 ;
;
(2)若复数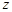 满足
满足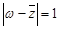 ,求
,求 的最小值.
的最小值.
某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售 、
、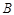 两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的大数据统计分析,
两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的大数据统计分析, 品牌的销售利润
品牌的销售利润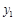 与投入资金
与投入资金 成正比,其关系如图1所示,
成正比,其关系如图1所示,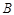 品牌的销售利润
品牌的销售利润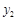 与投入资金
与投入资金 的算术平方根成正比,其关系如图2所示(利润与资金的单位:万元).
的算术平方根成正比,其关系如图2所示(利润与资金的单位:万元).
(1)分别将 、
、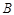 两个品牌的销售利润
两个品牌的销售利润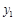 、
、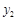 表示为投入资金
表示为投入资金 的函数关系式;
的函数关系式;
(2)该商场计划投入5万元经销该种商品,并全部投入 、
、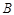 两个品牌,问:怎样分配这5万元资金,才能使经销该种商品获得最大利润,其最大利润为多少万元?
两个品牌,问:怎样分配这5万元资金,才能使经销该种商品获得最大利润,其最大利润为多少万元?
(1)找出一个等比数列 ,使得1,
,使得1, ,4为其中的三项,并指出分别是
,4为其中的三项,并指出分别是 的第几项;
的第几项;
(2)证明: 为无理数;
为无理数;
(3)证明:1, ,4不可能为同一等差数列中的三项.
,4不可能为同一等差数列中的三项.
已知定义在 上的函数
上的函数 是偶函数.
是偶函数.
(1)求实数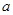 的值;
的值;
(2)判断 在
在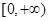 上的单调性,并用定义法证明;
上的单调性,并用定义法证明;
(3)若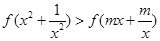 恒成立,求实数
恒成立,求实数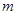 的取值范围
的取值范围
已知函数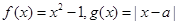 .
.
(1)当 时,求
时,求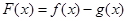 的零点;
的零点;
(2)若方程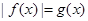 有三个不同的实数解,求
有三个不同的实数解,求 的值;
的值;
(3)求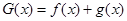 在
在 上的最小值
上的最小值 .[来
.[来