已知
是
的共轭复数，且
，则复数=（ ）
A． |
B． |
C． |
D． |
用反证法证明命题“三角形的内角中至少有一个不大于60度”时，反设正确的是 （ ）
| A．假设三个内角都不大于60度 |
| B．假设三个内角都大于60度 |
| C．假设三个内角至多有一个大于60度 |
| D．假设三个内角至多有两个大于60度 |
在区间
上的最大值是（ ）
| A．-2 | B．0 | C．2 | D．4 |
函数
在
处取到极值，则
的值为（ ）
A． |
B． |
C．0 | D． |
从集合{0，1，2，3，4，5，6}中任取两个互不相等的数
，
组成复数
，其中虚数有（ ）
| A．30个 | B．42个 | C．36个 | D．35个 |
由直线
，
，曲线
及
轴所围成的图形的面积是（ ）
A． |
B． |
C． |
D． |
函数
在点
处的切线方程是（ ）
A． |
B． |
C． |
D． |
给出下面四个类比结论：
①实数
，若
，则
或
；类比向量
，若
，则
或
②实数，有
；类比向量，有
③向量
，有
；类比复数
有
④实数，有
，则
；类比复数
，有
，则
其中类比结论正确的命题个数是（ ）
| A．0 | B．1 | C．2 | D．3 |
函数
（
,则（ ）
A． |
B． |
C． |
D． 大小关系不能确定 |
函数
的图象大致是（ ）
今有2个红球、3个黄球、4个白球，同色球不加以区分，将这9个球排成一列有 种不同的方法（用数字作答）;
一物体沿直线以速度
（
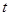的单位为:秒,
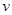的单位为:米/秒）的速度作变速直线运动，则该物体从时刻t=0秒至时刻 t=5秒间运动的路程是_______
下表给出了一个“三角形数阵”：
依照表中数的分布规律，可猜得第10行第6个数是
将10个学生干部的培训指标分配给7个不同的班级，每班至少分到一个名额，不同的分配方案共有_______种。
若函数
在区间
上是单调递增函数，则实数
的取值范围是_____．
已知复数
．
（Ⅰ）求
及
；
（Ⅱ）若
，求实数
的值．
已知函数
．
（Ⅰ）求函数
的单调递增区间；
（Ⅱ）求函数在
上的最大值和最小值．
已知
的展开式的前三项的系数成等差数列；
（1）求
展开式中所有的有理项；
（2）求
展开式中系数的绝对值最大的项。
根据某校五年发展规划，学校将修建一座长
米,宽
米的长方形体育馆．按照建筑要求,每隔
米需打建一个桩位,每个桩位需花费
万元（桩位视为一点且打在长方形的边上）,桩位之间的米墙面需花
万元,在不计地板和天花板的情况下,当为何值时,所需总费用最少？
在数列
中，已知
，且
。
（1）用数学归纳法证明：
；
（2）求证
．
已知
在
时有极值0。
（1）求常数 a,b的值；
（2）求f（x）的单调区间。
（3）方程f（x）=c在区间[-4,0]上有三个不同的实根时实数
的范围。