设
是虚数单位，则
= ．
写出命题“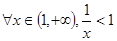
”的否定： ．
设
是虚数单位，则复数
的共轭复数
= ．
“
”是“
”的 条件．（请在“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选择一个合适的填空）
将演绎推理“函数
的图像是一条直线．”恢复成完全的三段论形式，其中大前提是 ．
设
是虚数单位，复数
满足
=1，则
的最大值为 ．
学校举办了排球赛，某班45名同学中有12名同学参赛．后来又举办了田径赛，该班有20名同学参赛．已知两项比赛中，该班有19名同学没有参加比赛，那么该班两项都参加的有 名同学．
设集合
，则满足
的集合B的个数是： ．
在R上定义运算⊙：
⊙
，则关于实数
的不等式：⊙
的解集为 ．
已知全集U=R，集合A=
，
，若
，则实数a的取值范围是 ．
设
是虚数单位，
，则实数
．
已知
，则
．
求“方程
的解”有如下解题思路：设
，则
在
上单调递减，且
，所以原方程有唯一解
．类比上述解题思路，方程
的解为 ．
下列说法正确的是 ．（填上所有正确答案的序号）
①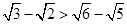
；
② 任何集合都有子集；
③ 实数没有共轭复数；
④ 命题“正三角形的三条边全相等．”的逆否命题是“如果一个三角形的三条边全不相等，那么这个三角形不是正三角形．”
（本小题满分14分）已知命题p：方程x2+mx+1=0有两个不相等的实根；q：不等式4x2+4（m–2）x+1>0的解集为R．
（1）若命题q为真，求实数m的取值范围．
（2）若命题“p且q”和“非p”为假，求实数m的取值范围
（本小题满分14分）（1）已知
，求实数
的值；
（2）已知
，若
是纯虚数，求
（本小题满分14分）已知集合
，
．
（1）当
时，求
；
（2）若
，求实数
的取值范围．
（本小题满分16分）图（1）、（2）、（3）、（4）分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”，按同样的方式构造图形，设第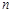
个图形包含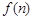
个“福娃迎迎”．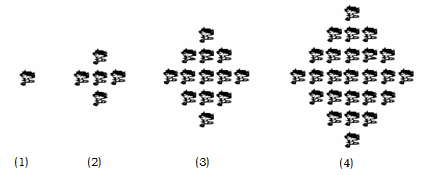
（1）求出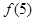
；
（2）利用合情推理的“归纳推理思想”归纳出
与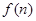
的关系式（不需写出证明过程）；
（3）根据你得到的关系式求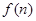的表达式．
已知二次函数f（x）=ax2+bx+c ．
（1） 设集合A={x|f（x）=x}．
①若A={1，2}，且f（0）=2，求f（x）的解析式；
②若A={1}，且a≥1，求f（x）在区间[﹣2，2]上的最大值M（a）．
（2） 设f（x）的图像与x轴有两个不同的交点，a>0， f（c）=0，且当0<x<c时，f（x）>0．用反证法证明：
．
（本小题满分16分）已知函数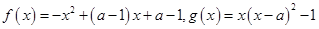
，其中a为实数．
（1）是否存在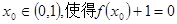
？若存在，求出实数a的取值范围；若不存在，请说明理由．
（2）若集合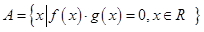
中恰有5个元素，求实数a的取值范围．