在实数－2、－
、－
、－3中，最大的实数是（ ）.
| A．－2 | B．－ |
C．－ |
D．－3 |
已知
＝
，则
的取值范围是（ ）.
| A．≤2 |
B．＜2 |
C．＞2 |
D．≥2 |
下列根式中属于最简二次根式的是（ ）.
A． |
B． |
C． |
D． |
△ABC中，下列条件一定不能判断△ABC为直角三角形的是（ ）.
A． |
B． ， ， |
| C．∠A:∠B:∠C=3:4:5 |
D．三边长分别为 ， ， ＞1) |
将
根号外的部分移到根号内，正确的是（ ）.
A． |
B． |
C． |
D． |
已知
、
分别是6+
和6-的小数部分，则式子
的值是（ ）.
| A．4 | B．3 | C．2 | D．1 |
如图，已知Rt△ABC中，∠BAC＝90°，AD⊥BC，BD＝9，CD＝16，下列选项结论中，此题数据不能验证的结论选项是（ ）.
A． |
B． |
C． |
D． |
如图，在Rt△ACD中，∠C＝90°，AC＝DC，以AD为直径的半圆面积为
，那么DC的长是（ ）.
A． |
B． |
C． |
D．无法确定 |
式子
化简的结果是（ ）.
A． |
B． |
C． |
D． |
如图，已知△ABC中，点D在AB上，且CD=AD＝BD，点F在BC上，过D作DE⊥DF交AC于E，过F作FG⊥AB于G，以下结论：①△ABC为直角三角形，②
，③
，④
，其中结论正确的序号是（ ）.
| A．①② | B．①④ | C．①②③ | D．①②③④ |
若式子
有意义，则
的取值范围是 .
在平面直角坐标系中，点P（－2，4）到
轴的距离是 ，到
轴的距离是 ，到原点的距离是 .
命题“如果两个实数相等，那么它们的立方值相等”的逆命题是 ，它是 （真或假）命题.
观察勾股数：3、4、5；8、6、10；15、8、17……则顺次第6组勾股数是 .
已知等边三角形的面积为
，其边长是 .
在平面直角坐标系中，A（-1，0），B（1，0），点P是坐标轴上的一点，要使△ABP是直角三角形，则P点的坐标是 .
（本题6分）在实数范围内分解因式：（1）
；（2）
.
（本题16分）计算：
（1）
；
（2）
－
；
（3）
；
（4）
.
（本题7分）如图，长方形纸片ABCD中，AD＝8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，EF＝3，求AB的长.
本题6分）如图，平面直角坐标系中，
（1）取点A（2，1）、点B（－3，4），则线段AB的长为 ；
（2）若点A的坐标为A（
，
），点B的坐标为A（
，
），则线段AB的长为 （用含、、、的式子表示）；
（3）△ABC中，已知点A（2，－2）、点B（－3，－1）、点C（－1、－4），请运用（2）中的结论，不画图，用代数方法判断并证明△ABC的形状.
（本题7分）化简求值.
已知：
，求式子
的值.
（本题8分）如图，四边形ABCD中，∠ABC＝90°，CD⊥AD，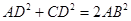
，
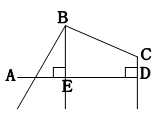
（1）求证：AB=BC；
（2）过点B作BE⊥AD于E，若四边形ABCD的面积为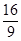
，求BE的长.
（本题10分）如图，已知四边形ABCD中，AD=4，CD＝3，AB=AC，
（1）如图1，若∠CAB＝60°，∠ADC＝30°，求BD的长；
（2）如图2，若∠CAB＝90°，∠ADC＝45°，求BD的长.
（本题12分）已知直线AB分别交
、
轴于A（4，0）、B两点，C（－4，
）为直线AB上且在第二象限内一点，若△COA的面积为8，
（1）如图1，求C点坐标；
（2）如图2，点M为第二象限内一点，CM⊥OM于M，CN⊥轴于N，连MN，求证：
的值；
（3）如图3，过C作CN⊥轴于N，G为第一象限内一点，且∠NGO＝45°，试探究GC2、GN2与GO2之间的数量关系并说明理由.