若 ,则下列不等式①
,则下列不等式① , ②
, ② ,③
,③ , ④
, ④ 中,正确的有( )
中,正确的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
命题“若 都是偶数,则
都是偶数,则 也是偶数”的逆否命题是( )
也是偶数”的逆否命题是( )
A.若 是偶数,则 是偶数,则 与 与 不都是偶数 不都是偶数 |
B.若 是偶数,则 是偶数,则 与 与 都不是偶数 都不是偶数 |
C.若 不是偶数,则 不是偶数,则 与 与 不都是偶数 不都是偶数 |
D.若 不是偶数,则 不是偶数,则 与 与 都不是偶数 都不是偶数 |
已知p:|x|<3;q:x2-x-2<0,则p是q的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若点 在第一象限且在直线
在第一象限且在直线 上移动,则
上移动,则 ( )
( )
| A.最大值为1 | B.最小值为1 |
| C.最大值为2 | D.没有最大、小值 |
已知等差数列{an}的公差d≠0,若 成等比数列,那么公比为( )
成等比数列,那么公比为( )
A. |
B. |
C. |
D. |
设变量 、
、 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
数列1,1+2,1+2+22, ,1+2+22+ + , 的前n项和为( )
, 的前n项和为( )
| A.2n-n-1 | B.2n+1-n-2 | C.2n | D.2n+1-n |
如果函数 对任意的实数
对任意的实数 ,存在常数
,存在常数 ,使得不等式
,使得不等式 恒成立,那么就称函数
恒成立,那么就称函数 为有界泛函.给出下面三个函数:①
为有界泛函.给出下面三个函数:① ;②
;② ;③
;③ .其中属于有界泛函的是( )
.其中属于有界泛函的是( )
| A.①③ | B.② | C.③ | D.①② |
写出命题P: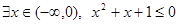 的否定
的否定 .
.
不等式 的解集为 .
的解集为 .
已知等比数列{an}的前n项和 ,则实数t的值为 .
,则实数t的值为 .
已知两个正实数 满足
满足 ,则使不等式
,则使不等式 +
+ ≥
≥ 恒成立的实数
恒成立的实数 的取值范围是 .
的取值范围是 .
给定下列四个命题:
①“ ”是“
”是“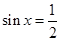 ”的充分不必要条件;
”的充分不必要条件;
②若am2<bm2, 则a<b;
③若三个实数 既是等差数列,又是等比数列,则
既是等差数列,又是等比数列,则  ;
;
④若不等式 的解集
的解集 则
则 =-10.
=-10.
其中为真命题的是 .(填上所有正确命题的序号)
在平面直角坐标系上,设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为 .则
.则 = ,经猜想可得到
= ,经猜想可得到 = .
= .
(本小题满分12分)设数列 的前
的前 项和为
项和为 ,数列
,数列 为等比数列,且
为等比数列,且 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)已知命题p:∀x∈[1,2],x2-a 0.命题q:∃x0∈R,使得x02+(a-1)x0+1=0.若“p或q”为真,“p且q”为假,求实数a的取值范围.
0.命题q:∃x0∈R,使得x02+(a-1)x0+1=0.若“p或q”为真,“p且q”为假,求实数a的取值范围.
(本小题满分14分)已知函数
(Ⅰ)当 时,求函数
时,求函数 的最小值;
的最小值;
(Ⅱ)若对任意 ,
, 恒成立,试求实数
恒成立,试求实数 的取值范围
的取值范围
(本小题满分15分)已知数列 的首项
的首项 ,
, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前n项和
的前n项和 ;
;
(3)求证: ,
, .
.
(本小题满分12分)某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗 原料1千克、
原料1千克、 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗 原料2千克,
原料2千克, 原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗 、
、 原料都不超过12千克.如何合理安排生产计划 ,使公司可获得最大利润?最大利润为多少?
原料都不超过12千克.如何合理安排生产计划 ,使公司可获得最大利润?最大利润为多少?
(本小题满分15分)在数列 中,已知
中,已知 ,其前n项和
,其前n项和 满足
满足 .
.
(1)求 的值;
的值;
(2)求数列 的通项公式
的通项公式 ;
;
(3)令 ,试求一个函数
,试求一个函数 ,使得对于任意正整数n,
,使得对于任意正整数n, ,且对于任意的
,且对于任意的 ,均存在
,均存在 ,使得
,使得 时,
时, .
.