设全集U=R,集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
设 为两条不同的直线,
为两条不同的直线, 为两个不同的平面,下列命题中为真命题的是( )
为两个不同的平面,下列命题中为真命题的是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则 ,则 |
D.若 ,则 ,则 |
已知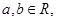 则“
则“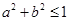 ”是“
”是“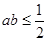 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知 的图象的一部分如图所示,若对任意
的图象的一部分如图所示,若对任意 都有
都有 , 则
, 则 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
已知实数变量 满足
满足 则
则 的最大值为 ( )
的最大值为 ( )
| A.1 | B.2 | C.3 | D.4 |
设等差数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,对任意正整数
,对任意正整数 ,都有
,都有 ,则
,则 的值为( )
的值为( )
| A.1006 | B.1007 | C.1008 | D.1009 |
设 分别是双曲线
分别是双曲线 的左、右焦点,
的左、右焦点, 是
是 的右支上的点,射线
的右支上的点,射线 平分
平分 ,过原点
,过原点 作
作 的平行线交
的平行线交 于点
于点 ,若
,若 ,则
,则 的离心率为( )
的离心率为( )
A. |
B.3 | C. |
D. |
已知实数 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
若指数函数 的图像过点
的图像过点 ,则
,则 _____________;不等式
_____________;不等式 的解集为 .
的解集为 .
已知圆 的圆心在直线
的圆心在直线 上,则
上,则 ;圆
;圆 被直线
被直线 截得的弦长为____________.
截得的弦长为____________.
某多面体的三视图如图所示,则该多面体最长的棱长为 ;外接球的体积为 .
“斐波那契数列”是数学史上一个著名数列,在斐波那契数列 中,
中, ,
, …
… 则
则 ____________;若
____________;若 ,则数列
,则数列 的前
的前 项和是____________(用
项和是____________(用 表示).
表示).
已知函数 ,若关于
,若关于 的方程
的方程 有4个不同的实数根,则
有4个不同的实数根,则 的取值范围是________________.
的取值范围是________________.
定义:曲线 上的点到点
上的点到点 的距离的最小值称为曲线
的距离的最小值称为曲线 到点
到点 的距离。已知圆
的距离。已知圆 到点
到点 的距离为
的距离为 ,则实数
,则实数 的值为 .
的值为 .
设正 的面积为2,边
的面积为2,边 的中点分别为
的中点分别为 ,
, 为线段
为线段 上的动点,则
上的动点,则 的最小值为_____________.
的最小值为_____________.
在 中,内角
中,内角 所对的边分别为
所对的边分别为 已知
已知 ,
,
(Ⅰ)求角 的取值范围;
的取值范围;
(Ⅱ)若 的面积
的面积 ,
, 为钝角,求角
为钝角,求角 的大小.
的大小.
如图,在三棱锥 中,
中, ,
, ,
, ,
, 。
。
(Ⅰ)平面 平面
平面 ;
;
(Ⅱ) 为
为 上的一点.若直线
上的一点.若直线 与平面
与平面 所成的角为
所成的角为 ,求
,求 的长.
的长.
已知数列 满足下列条件:
满足下列条件:
 ,
,
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)比较 与
与 的大小.
的大小.
如图,过抛物线 的焦点
的焦点 的直线交
的直线交 于
于 两点,且
两点,且

(Ⅰ)求 的值;
的值;
(Ⅱ) 是
是 上的两动点,
上的两动点, 的纵坐标之和为1,
的纵坐标之和为1, 的垂直平分线交
的垂直平分线交 轴于点
轴于点 ,求
,求 的面积的最小值.
的面积的最小值.
已知函数 ,其中
,其中 为实常数.
为实常数.
(Ⅰ)判断 的奇偶性;
的奇偶性;
(Ⅱ)若对任意 ,使不等式
,使不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.