已知集合 ,则
,则 .
.
设复数 满足
满足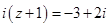 ,则
,则 = .
= .
命题“ ,
,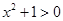 ”的否定是 .
”的否定是 .
已知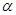 为第三象限角,且
为第三象限角,且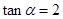 ,则
,则 .
.
从3名男同学,2名女同学中任选2人参加体能测试,则选到的2名同学中至少有一名男同学的概率是 .
已知向量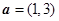 ,
, ,
,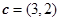 .若向量
.若向量 与向量
与向量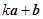 共线,则实数
共线,则实数 .
.
锐角 中角
中角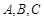 的对边分别是
的对边分别是 ,
,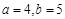 ,
,  的面积为
的面积为 , 则
, 则 .
.
用半径为 的半圆形铁皮卷成一个圆锥的侧面,则此圆锥的体积是 .
的半圆形铁皮卷成一个圆锥的侧面,则此圆锥的体积是 .
已知等比数列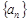 的前
的前 项和为
项和为 ,若
,若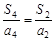 ,则
,则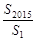 等于 .
等于 .
若函数 的图象过点
的图象过点 ,则该函数图象在
,则该函数图象在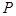 点处的切线倾斜角等于 .
点处的切线倾斜角等于 .
若直线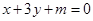 截半圆
截半圆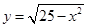 所得的弦长为
所得的弦长为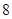 ,则
,则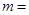 .
.
平面内四点 满足
满足 ,则
,则 面积的最大值为 .
面积的最大值为 .
已知椭圆E: 的右焦点为F,离心率为
的右焦点为F,离心率为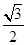 ,过原点O且倾斜角为
,过原点O且倾斜角为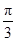 的直线
的直线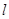 与椭圆E相交于A、B两点,若△AFB的周长为
与椭圆E相交于A、B两点,若△AFB的周长为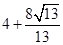 ,则椭圆方程为 .
,则椭圆方程为 .
已知函数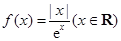 ,
, , 若
, 若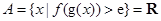 ,则
,则 的取值范围是 .
的取值范围是 .
如图,三棱锥 中,侧面
中,侧面 是等边三角形,
是等边三角形, 是
是 的中心.
的中心.
(1)若 ,求证
,求证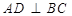 ;
;
(2)若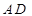 上存在点
上存在点 ,使
,使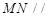 平面
平面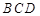 ,求
,求 的值.
的值.
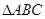 的内角
的内角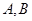 满足
满足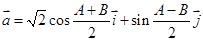 (单位向量
(单位向量 互相垂直),且
互相垂直),且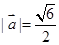 .
.
(1)求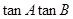 的值;
的值;
(2)若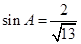 ,边长
,边长 ,求边长
,求边长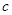 .
.
一件要在展览馆展出的文物近似于圆柱形,底面直径为0.8米,高1.2米,体积约为0.6立方米.为保护文物需要设计各面是玻璃平面的正四棱柱形无底保护罩,保护罩底面边长不少于1.2米,高是底面边长的2倍.保护罩内充满保护文物的无色气体,气体每立方米500元.为防止文物发生意外,展览馆向保险公司进行了投保,保险费用与保护罩的占地面积成反比例,当占地面积为1平方米时,保险费用为48000元.
(1)若保护罩的底面边长为 米,求气体费用与保险费用的和;
米,求气体费用与保险费用的和;
(2)为使气体费用与保险费用的和最低,保护罩应如何设计?
已知椭圆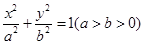 的左顶点为
的左顶点为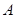 ,右焦点为
,右焦点为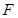 ,右准线为
,右准线为 ,
, 与
与 轴相交于点
轴相交于点 ,且
,且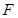 是
是 的中点.
的中点.
(1)求椭圆的离心率;
(2)过点 的直线与椭圆相交于
的直线与椭圆相交于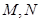 两点,
两点,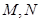 都在
都在 轴上方,并且
轴上方,并且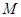 在
在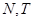 之间,且
之间,且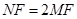 .
.
①记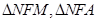 的面积分别为
的面积分别为 ,求
,求 ;
;
②若原点 到直线
到直线 的距离为
的距离为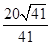 ,求椭圆方程.
,求椭圆方程.
设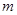 个正数
个正数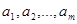
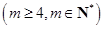 依次围成一个圆圈.其中
依次围成一个圆圈.其中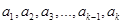
 是公差为
是公差为 的等差数列,而
的等差数列,而 是公比为
是公比为 的等比数列.
的等比数列.
(1)若 ,
,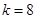 ,求数列
,求数列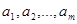 的所有项的和
的所有项的和 ;
;
(2)若 ,
, ,求
,求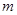 的最大值;
的最大值;
(3)是否存在正整数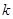 ,满足
,满足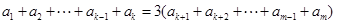 ?若存在,求出
?若存在,求出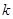 值;
值;
若不存在,请说明理由.
设函数 ,
,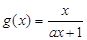 (其中
(其中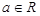 ,
, 是自然对数的底数).
是自然对数的底数).
(1)若函数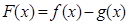 没有零点,求实数
没有零点,求实数 的取值范围;
的取值范围;
(2)若函数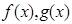 的图象有公共点
的图象有公共点 ,且在点
,且在点 有相同的切线,求实数
有相同的切线,求实数 的值;
的值;
(3)若 在
在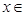
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知矩阵 ,计算
,计算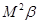 .
.
已知圆 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为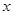 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是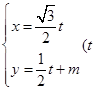 是参数).若直线
是参数).若直线 与圆
与圆 相切,求正数
相切,求正数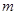 的值.
的值.
如图,平行四边形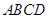 所在平面与直角梯形
所在平面与直角梯形 所在平面互相垂直,且
所在平面互相垂直,且 ,
, 为
为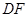 中点.
中点.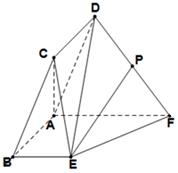
(1)求异面直线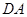 与
与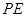 所成的角;
所成的角;
(2)求平面 与平面
与平面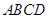 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
设集合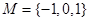 ,集合
,集合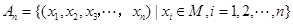 ,
,
集合 中满足条件“
中满足条件“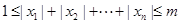 ”的元素个数记为
”的元素个数记为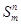 .
.
(1)求 和
和 的值;
的值;
(2)当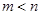 时,求证:
时,求证: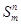
 .
.