否定“自然数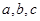 中恰有一个偶数”时正确的反设为
中恰有一个偶数”时正确的反设为
A.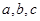 都是奇数 都是奇数 |
B.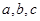 都是偶数 都是偶数 |
C.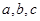 至少有两个偶数 至少有两个偶数 |
D.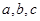 至少有两个偶数或者都是奇数 至少有两个偶数或者都是奇数 |
下列正确的是
A. |
B.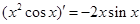 |
C.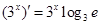 |
D.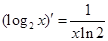 |
在等差数列 中,
中,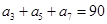 ,则
,则 等于
等于
A.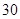 |
B.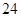 |
C. |
D.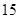 |
设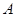 是
是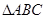 的最小内角,则
的最小内角,则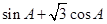 的取值范围为
的取值范围为
A.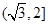 |
B.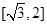 |
C. |
D.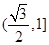 |
在等比数列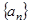 中,
中, ,那么
,那么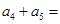
A.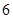 |
B.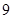 |
C.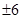 |
D. |
在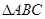 中,
中,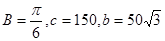 ,则
,则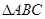 为
为
| A.直角三角形 | B.等腰三角形或直角三角形 |
| C.等边三角形 | D.等腰三角形 |
设数列 是等差数列,
是等差数列,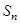 是
是 的前
的前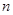 项和,且
项和,且 ,则下列结论错误的是
,则下列结论错误的是
A. |
B.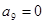 |
C. 均为 均为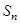 的最小值 的最小值 |
D.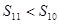 |
若 ,则
,则
A. |
B.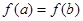 |
C.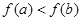 |
D.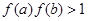 |
已知数列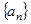 是首项为
是首项为 的等比数列,
的等比数列, 是
是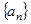 的前
的前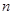 项和,且
项和,且 ,则数列
,则数列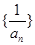 的前
的前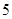 项和为
项和为
A.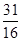 或 或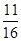 |
B.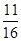 或 或 |
C.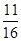 |
D.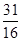 |
设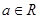 ,若函数
,若函数
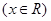 有大于
有大于 的极值点,则
的极值点,则
A.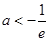 |
B. |
C. |
D. |
函数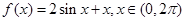 的单调增区间为 .
的单调增区间为 .
将长为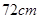 的铁丝截成
的铁丝截成 段,搭成一个正四棱柱的模型,以此为骨架做成一个容积最大的容器,则此四棱柱的高应该是
段,搭成一个正四棱柱的模型,以此为骨架做成一个容积最大的容器,则此四棱柱的高应该是 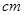 .
.
某地区恩格尔系数(表示生活水平高低的一个指标)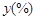 与年份
与年份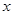 的统计数据如下表:
的统计数据如下表:
年份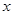 |
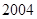 |
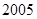 |
 |
 |
恩格尔系数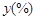 |
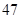 |
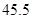 |
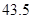 |
 |
从散点图可以看出 与
与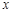 线性相关,且可得回归直线方程为
线性相关,且可得回归直线方程为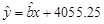 ,据此模型可预测
,据此模型可预测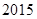 年该地区的恩格尔系数为
年该地区的恩格尔系数为  .
.
已知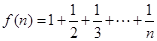 .经计算得
.经计算得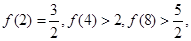
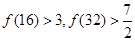 ,由此可推得一般性结论为 .
,由此可推得一般性结论为 .
在 中,角
中,角 的对边分别为
的对边分别为 ,若角
,若角 依次成等差数列,且
依次成等差数列,且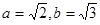 ,则
,则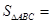 .
.
(1)某企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了 名员工进行调查,所得的数据如下表所示:
名员工进行调查,所得的数据如下表所示:
| |
积极支持改革 |
不太支持改革 |
合 计 |
| 工作积极 |
 |
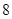 |
 |
| 工作一般 |
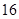 |
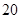 |
 |
| 合 计 |
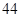 |
 |
 |
对于人力资源部的研究项目,根据上述数据你能得出什么结论?
(友情提示:当 时,有
时,有 的把握说事件
的把握说事件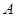 与
与 有关;当
有关;当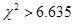 时,有
时,有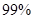 的把握说事件
的把握说事件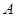 与
与 有关; 当
有关; 当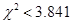 时认为事件
时认为事件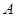 与
与 无关.)
无关.)
(2)高中数学必修3第三章内容是概率.概率包括事件与概率,古典概型,概率的应用.事件与概率又包括随机现象,事件与基本事件空间,频率与概率,概率的加法公式.请画出它们之间的知识结构图.
已知 分别为
分别为 三个内角
三个内角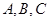 的对边,且
的对边,且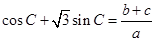 .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,且
,且 ,
,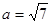 ,求
,求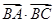 的值.
的值.
已知曲线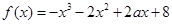 在
在 处切线与直线
处切线与直线 垂直.
垂直.
(Ⅰ)求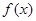 解析式;
解析式;
(Ⅱ)求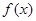 的单调区间、极值并画出
的单调区间、极值并画出 的大致图象.
的大致图象.
当 且
且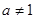 时,判断
时,判断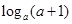 与
与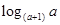 的大小,并给出证明.
的大小,并给出证明.
已知数列 的前
的前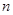 项和为
项和为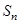 ,
,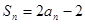 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前
的前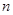 项和为
项和为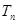 ,
,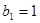 ,点
,点 在直线
在直线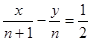 上,若存在
上,若存在 ,使不等式
,使不等式 成立,求实数
成立,求实数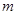 的最大值.
的最大值.
设函数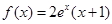 (其中
(其中 ).
).
(Ⅰ)求函数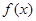 的极值;
的极值;
(Ⅱ)求函数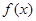 在
在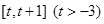 上的最小值;
上的最小值;
(Ⅲ)若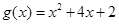 ,判断函数
,判断函数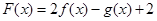 零点个数.
零点个数.