已知集合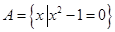 ,集合
,集合 ,则
,则 .
.
若复数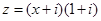 是纯虚数,其中
是纯虚数,其中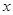 为实数,
为实数,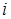 为虚数单位,则
为虚数单位,则 的共轭复数
的共轭复数 .
.
根据如图所示的伪代码,则输出的 的值为 .
的值为 .
若抛物线 的焦点
的焦点 与双曲线
与双曲线 的一个焦点重合,则
的一个焦点重合,则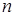 的值为 .
的值为 .
某单位有840名职工, 现采用系统抽样抽取42人做问卷调查, 将840人按1, 2, …, 840随机编号, 则抽取的42人中, 编号落入区间[61, 120]的人数为 .
某公司从四名大学毕业生甲、乙、丙、丁中录用两人,若这四人被录用的机会均等,则甲与乙中至少有一人被录用的概率为 .
若 满足约束条件
满足约束条件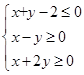 , 则目标函数
, 则目标函数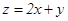 的最大值为 .
的最大值为 .
已知正四棱锥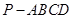 的体积为
的体积为 ,底面边长为
,底面边长为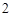 ,则侧棱
,则侧棱 的长为 .
的长为 .
若角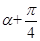 的顶点为坐标原点,始边与
的顶点为坐标原点,始边与 轴的非负半轴重合,终边在直线
轴的非负半轴重合,终边在直线 上,则
上,则 的值为 .
的值为 .
动直线 与曲线
与曲线 相交于
相交于 ,
, 两点,
两点, 为坐标原点,当
为坐标原点,当 的面积取得最大值时,
的面积取得最大值时, 的值为 .
的值为 .
若函数 ,则
,则 是函数
是函数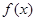 为奇函数的 条件.(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
为奇函数的 条件.(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
在边长为1的菱形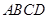 中,
中, ,若点
,若点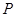 为对角线
为对角线 上一点,则
上一点,则 的最大值为 .
的最大值为 .
设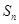 是等差数列
是等差数列 的前
的前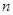 项和,若数列
项和,若数列 满足
满足 且
且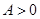 ,则
,则 的最小值为 .
的最小值为 .
若函数 有两个极值点
有两个极值点 ,其中
,其中 ,且
,且 ,则方程
,则方程 的实根个数为 .
的实根个数为 .
(本小题满分14分)已知 ,
, ,记函数
,记函数 .
.
(1)求函数 取最大值时
取最大值时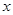 的取值集合;
的取值集合;
(2)设 的角
的角 所对的边分别为
所对的边分别为 ,若
,若 ,
,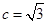 ,求
,求 面积的最大值.
面积的最大值.
(本小题满分14分)在直三棱柱 中,
中,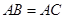 ,
, ,点
,点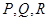 分别是棱
分别是棱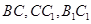 的中点.
的中点.
(1)求证: //平面
//平面 ;
;
(2)求证:平面
 平面
平面 .
.
(本小题满分14分)某地拟建一座长为 米的大桥
米的大桥 ,假设桥墩等距离分布,经设计部门测算,两端桥墩
,假设桥墩等距离分布,经设计部门测算,两端桥墩 、
、 造价总共为
造价总共为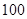 万元,当相邻两个桥墩的距离为
万元,当相邻两个桥墩的距离为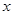 米时(其中
米时(其中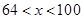 ),中间每个桥墩的平均造价为
),中间每个桥墩的平均造价为 万元,桥面每1米长的平均造价为
万元,桥面每1米长的平均造价为 万元.
万元.
(1)试将桥的总造价表示为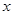 的函数
的函数 ;
;
(2)为使桥的总造价最低,试问这座大桥中间(两端桥墩 、
、 除外)应建多少个桥墩?
除外)应建多少个桥墩?
(本小题满分16分)如图,在平面直角坐标系 中,椭圆
中,椭圆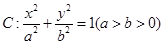 的离心率为
的离心率为 ,直线
,直线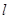 与
与 轴交于点
轴交于点 ,与椭圆
,与椭圆 交于
交于 、
、 两点.当直线
两点.当直线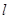 垂直于
垂直于 轴且点
轴且点 为椭圆
为椭圆 的右焦点时, 弦
的右焦点时, 弦 的长为
的长为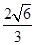 .
.
(1)求椭圆 的方程;
的方程;
(2)若点 的坐标为
的坐标为 ,点
,点 在第一象限且横坐标为
在第一象限且横坐标为 ,连结点
,连结点 与原点
与原点 的直线交椭圆
的直线交椭圆 于另一点
于另一点 ,求
,求 的面积;
的面积;
(3)是否存在点 ,使得
,使得 为定值?若存在,请指出点
为定值?若存在,请指出点 的坐标,并求出该定值;若不存在,请说明理由.
的坐标,并求出该定值;若不存在,请说明理由.
(本小题满分16分)设函数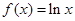 ,
, .
.
(1)当 时,函数
时,函数 与
与 在
在 处的切线互相垂直,求
处的切线互相垂直,求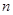 的值;
的值;
(2)若函数 在定义域内不单调,求
在定义域内不单调,求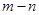 的取值范围;
的取值范围;
(3)是否存在实数 ,使得
,使得 对任意正实数
对任意正实数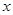 恒成立?若存在,求出满足条件的实数
恒成立?若存在,求出满足条件的实数 ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题满分16分)设函数 (其中
(其中 ),且存在无穷数列
),且存在无穷数列 ,使得函数在其定义域内还可以表示为
,使得函数在其定义域内还可以表示为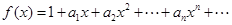 .
.
(1)求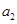 (用
(用 表示);
表示);
(2)当 时,令
时,令 ,设数列
,设数列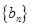 的前
的前 项和为
项和为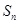 ,求证:
,求证: ;
;
(3)若数列 是公差不为零的等差数列,求
是公差不为零的等差数列,求 的通项公式.
的通项公式.
(选修4—1:几何证明选讲)
在 中,已知
中,已知 是
是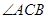 的平分线,
的平分线,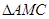 的外接圆交
的外接圆交 于点
于点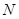 .若
.若 ,
, ,求
,求 的长.
的长.
(选修4—2:矩阵与变换)
若矩阵 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为 ,求矩阵
,求矩阵 的逆矩阵
的逆矩阵 .
.
(选修4—4:坐标系与参数方程)
在极坐标系中,曲线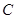 的极坐标方程为
的极坐标方程为 ,以极点
,以极点 为原点,极轴为
为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线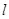 的参数方程为
的参数方程为 (
( 为参数),试判断直线
为参数),试判断直线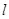 与曲线
与曲线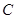 的位置关系,并说明理由.
的位置关系,并说明理由.
(选修4-5:不等式选讲)
已知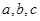 为正实数,求证:
为正实数,求证: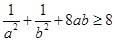 ,并求等号成立的条件.
,并求等号成立的条件.
(本小题满分10分)如图,已知四棱锥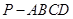 的底面是菱形,对角线
的底面是菱形,对角线 交于点
交于点 ,
,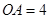 ,
,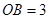 ,
, ,
, 底面
底面 ,设点
,设点 满足
满足 .
.
(1)当 时,求直线
时,求直线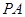 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(2)若二面角 的大小为
的大小为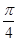 ,求
,求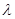 的值.
的值.
(本小题满分10分)设 .
.
(1)若数列 的各项均为1,求证:
的各项均为1,求证: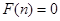 ;
;
(2)若对任意大于等于2的正整数 ,都有
,都有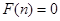 恒成立,试证明数列
恒成立,试证明数列 是等差数列.
是等差数列.