下列运算正确的是（ ）
A． |
B． |
C． |
D． |
描述一组数据离散程度的统计量是（ ）
| A．平均数 | B．众数 | C．中位数 | D．方差 |
在三边分别为下列长度的三角形中，不是直角三角形的是（ ）
| A．9，12，15 | B．1， ， |
C．2，3， |
D．4，7，5 |
在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）
下列命题错误的是（ ）
| A．对角线互相垂直平分的四边形是菱形 |
| B．平行四边形的对角线互相平分 |
| C．矩形的对角线相等 |
| D．对角线相等的四边形是矩形 |
如图，直线
与
（
）的交点的横坐标为
，则关于x的不等式
的整数解为（ ）
A． |
B． |
C． |
D． |
如图，△ABC≌△DCB，若∠A=75°，∠ACB=45°，则∠BCD等于（ ）．
| A．80° | B．60° | C．40° | D．20° |
若关于x的方程 
无解，则m的值为（ ）
| A．－1．5 | B．1 |
| C．－1．5或2 | D．－0．5或－1．5 |
如果三角形的一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（ ）
| A．1,2,3 | B．1,1， |
C．1,1， |
D．1，，2 |
如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE最小，则这个最小值为（ ）
A． |
B． |
C．3 | D． |
一次函数
的图像经过点（2，－3），则m= ．
分解因式：
= ．
下图是由射线AB，BC，CD，DE，EA组成的平面图形，则∠1＋∠2＋∠3＋∠4＋∠5＝ ．
若一组数据1，2，x，4的众数是1，则这组数据的方差为 ．
直线
沿y轴向下平移5个单位，则平移后直线与y轴的交点坐标为 ．
如图，在□ABCD中，BE平分∠ABC，BC=6，DE="2" ，则□ABCD周长等于 ．
已知
，则
= ．
如图，四边形ABCD与四边形AEFG都是菱形，点C在AF上，点E，G分别在BC，CD上，若∠BAD=1350，∠EAG=750，则
= ．
在△ABC 中，AB=13cm，AC=20cm，BC 边上的高为12cm，则△ABC 的面积为 
．
如图，由全等三角形拼出的一系列图形中，第n个图形由n+1个全等三角形拼成，则第4个图形中平行四边形的个数为 ；第2n－1个图形中平行四边形的个数为 ．
……
计算（每小题5分，共10分）：
（1）
；
（2）
．
（本题8分）已知，如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE，AC平分∠BAD．求证：四边形ABCD为菱形．
（本题10分）如图，四边形ABCD中，∠ABC＝90°，CD⊥AD，
，
（1）求证：AB=BC；
（2）过点B作BE⊥AD于E，若四边形ABCD的面积为
，求BE的长．
如图，直线l上有一点P1（2，1），将点P1先向右平移1个单位，再向上平移2个单位得到像点P2，点P2恰好在直线l上．
（1）写出点P2的坐标；
（2）求直线l所表示的一次函数的表达式；
（3）若将点P2先向右平移3个单位，再向上平移6个单位得到像点P3．请判断点P3是否在直线l上，并说明理由．
（本题10分）在△ABC中，BC＝a，AC＝b，AB＝c，若∠C＝90°，如图（1），则根据勾股定理，得a2＋b2＝c2．若△ABC不是直角三角形，如图（2）和（3），请你类比勾股定理，试猜想a2＋b2与c2的关系，并证明你的结论．
（本题12分）为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了统计表和统计图：
甲、乙射击成绩统计表
| |
平均数 |
中位数 |
方差 |
命中10环的次数 |
| 甲 |
7 |
|
|
0 |
| 乙 |
|
|
|
1 |
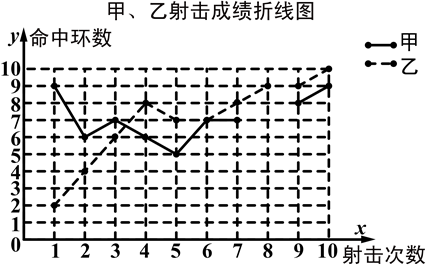
（1）请补全上述图表（直接在表中填空和补全折线图）；
（2）如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由；
（3）如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？