设集合A=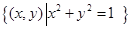 ,B=
,B=  ,则A
,则A B子集的个数是( )
B子集的个数是( )
| A.1 | B.2 | C.3 | D.4 |
在下列关于直线 、
、 与平面
与平面 、
、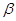 的命题中,正确的是 ( )
的命题中,正确的是 ( )
A.若 且 且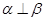 ,则 ,则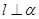 |
B.若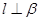 且 且 ,则 ,则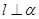 |
C.若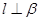 且 且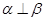 ,则 ,则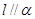 |
D.若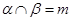 且 且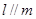 ,则 ,则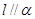 |
过点 和点
和点 的直线的倾斜角是 ( )
的直线的倾斜角是 ( )
A.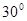 |
B. |
C.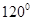 |
D. |
“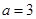 ”是“直线
”是“直线 与直线
与直线 平行”的( )
平行”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
当x>3时,不等式x+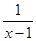 ≥
≥ 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
| A.(-∞,3] | B.[3,+∞) |
C.[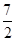 ,+∞) ,+∞) |
D.(-∞,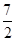 ] ] |
锐角 中,已知
中,已知 ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A. |
B.  |
C.  |
D. |
若等差数列 前
前 项和
项和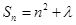 ,则
,则 = ( )
= ( )
| A.1 | B.-1 | C.0 | D.任意实数 |
一个几何体的三视图如图所示,则该几何体的体积的是( )

A.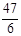 |
B. |
C. |
D. |
已知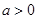 ,实数
,实数 满足:
满足: ,若
,若 的最小值为1,则
的最小值为1,则 ( )
( )
| A.2 | B.1 | C. |
D. |
 中三边上的高依次为
中三边上的高依次为 ,则
,则 为( )
为( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不存在这样的三角形 |
若直线 :
: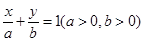 经过点
经过点 ,则直线
,则直线 在
在 轴和
轴和 轴的截距之和的最小值是_______.
轴的截距之和的最小值是_______.
在数列{an}中,a1=2,an+an+1=1(n∈N*),设Sn为数列{an}的前n项和,则S2007-2S2006+S2005的值为________.
在 中,内角
中,内角 的对边分别为
的对边分别为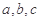 ,
, 已知,且
已知,且 ,则
,则 的面积是 .
的面积是 .
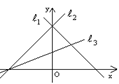
如图所示,直线 的斜率分别为
的斜率分别为 ,则
,则 的大小关系为 (按从大到小的顺序排列).
的大小关系为 (按从大到小的顺序排列).
如图,正四棱柱 (底面是正方形的直棱柱)的底面边长为2,高为4,那么异面直线
(底面是正方形的直棱柱)的底面边长为2,高为4,那么异面直线 与AD所成角的正切值______________.
与AD所成角的正切值______________.
若 ,
, ,
, 是实数,则
是实数,则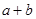 的最大值是 .
的最大值是 .
(本题10分)已知直线l:x+2y-2=0,试求:
(1)点P(-2,-1)关于直线l的对称点坐标;
(2)直线l1:y=x-2关于直线l对称的直线l2的方程;
(3)直线l关于点(1,1)对称的直线方程.
(本题10分)已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,PA⊥平面ABCD.
(1)求证:PF⊥FD;
(2)设点G在PA上,且EG//平面PFD,试确定点G的位置.
在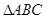 中,
中, 的对边分别为
的对边分别为 ,已知
,已知
(Ⅰ)求 的值;
的值;
(Ⅱ)若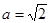 ,求
,求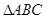 的面积.
的面积.
已知数列{an}为等差数列,a3=5,a7=13,数列{bn}的前n项和为Sn,且有Sn=2bn-1,
(1)求{an},{bn}的通项公式.
(2)若cn=anbn,{cn}的前n项和为Tn,求Tn.