设集合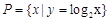 ,
,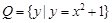 ,则
,则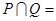 ( )
( )
A. |
B. |
C.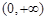 |
D. |
设等比数列 中,公比
中,公比 ,前
,前 项和为
项和为 ,则
,则 的值为( )
的值为( )
A.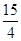 |
B. |
C. |
D. |
在 中,若
中,若 ,则
,则 是( )
是( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.无法确定 |
“k=5”是“两直线kx+5y-2=0和(4-k)x+y-7=0互相垂直”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题中正确的是( )
A.当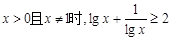 |
B.当 , ,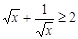 |
C.当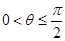 , , 的最小值为 的最小值为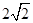 |
D.当 无最大值 无最大值 |
若直线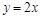 上存在点(x,y)满足约束条件
上存在点(x,y)满足约束条件 ,则实数m的最大值为( )
,则实数m的最大值为( )
A. |
B.1 | C. |
D.2 |
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面四个命题中不正确的是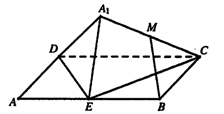
| A.|BM|是定值 |
| B.点M在某个球面上运动 |
| C.存在某个位置,使DE⊥A1 C |
| D.存在某个位置,使MB//平面A1DE |
已知直线l的倾斜角为 ,直线
,直线 经过点A(3,2),B(a,-1),且
经过点A(3,2),B(a,-1),且 与l垂直,直线
与l垂直,直线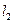 :2x+by+1=0与直线
:2x+by+1=0与直线 平行,则a+b=( ).
平行,则a+b=( ).
| A.-4 | B.-2 | C.0 | D.2 |
已知某几何体的三视图如图所示,其中网格纸的小正方形的边长是1,则该几何体 的表面积为( )

| A.4 | B. |
C. |
D.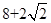 |
设 ,若
,若 是
是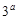 与
与 的等比中项,则
的等比中项,则 的最小值为( ).
的最小值为( ).
A. |
B. |
C. |
D. |
过点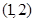 且垂直于直线
且垂直于直线 的直线
的直线 的方程为 .
的方程为 .
如图,在长方体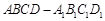 中,
中,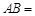 3 cm,
3 cm, 2 cm,
2 cm, 1 cm,则三棱锥
1 cm,则三棱锥 的体积为 cm3.
的体积为 cm3.
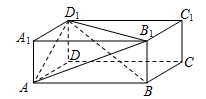
如图,在 中,
中, 是
是 边上一点,
边上一点, ,则
,则 的长为 .
的长为 .
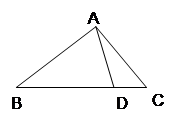
两等差数列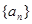 和
和 ,前
,前 项和分别为
项和分别为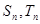 ,且
,且 则
则 等于 .
等于 .
设x,y,z均为正整数,满足x-2y+3z=0,则 的最小值是________.
的最小值是________.
如图是棱长为 的正方体的平面展开图,则在原正方体中,
的正方体的平面展开图,则在原正方体中,

① 平面
平面 ;
;
② 平面
平面 ;
;
③CN与BM成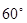 角;
角;
④DM与BN垂直.
⑤与该正方体各棱相切的球的表面积为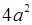 。
。
以上五个命题中,正确命题的序号是____ ____。
(写出所有正确命题的序号)
(本小题满分10分)已知两直线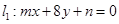 和直线
和直线 ,试确定
,试确定 的值,使
的值,使
(1) 和
和 相交于点
相交于点 ;
;
(2)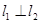 且
且 在y轴上的截距为
在y轴上的截距为 .
.
(本题10分)如图,ABCD是正方形,O是正方形的中心,PO 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE
(2)平面PAC 平面BDE
平面BDE
(本小题满分13分)设△ABC的内角A、B、C的对边长分别为a、b、c,设S为△ABC的面积,满足 .
.
(Ⅰ)求B;
(Ⅱ)若 ,设
,设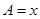 ,
, ,求函数
,求函数 的解析式和最大值.
的解析式和最大值.
(本小题满分13分)已知等差数列 的公差
的公差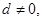 它的前
它的前 项和为
项和为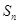 ,若
,若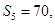 且
且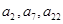 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,求证:
,求证: