有一段演绎推理:“直线平行于平面,则这条直线平行于平面内所有直线;已知直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 ∥平面
∥平面 ,则直线
,则直线 ∥直线
∥直线 ”的结论是错误的,这是因为( )
”的结论是错误的,这是因为( )
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.非以上错误 |
根据如下样本数据得到的回归方程为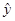 =bx+a,则( )
=bx+a,则( )
| x |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4.0 |
2.5 |
-0.5 |
0.5 |
-2.0 |
-3.0 |
A.a>0,b<0 B.a>0,b>0 C.a<0,b<0 D.a<0,b>0
已知随机变量 的分布列是其中
的分布列是其中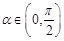 ,则
,则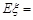
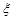 |
-1 |
0 |
2 |
| P |
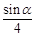 |
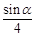 |
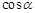 |
A、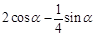 B、
B、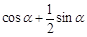 C、0 D、1
C、0 D、1
已知随机变量ξ服从正态分布N(1,σ2),若P(ξ>3)=0.023,则P(-1≤ξ≤3)等于( )
| A.0.977 | B.0.954 | C.0.628 | D.0.477 |
下面四个命题中,
① 复数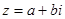 ,则实部、虚部分别是
,则实部、虚部分别是 ;
;
② 复数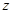 满足
满足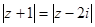 ,则
,则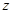 对应的点集合构成一条直线;
对应的点集合构成一条直线;
③ 由向量 的性质
的性质 ,可类比得到复数
,可类比得到复数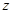 的性质
的性质 ;
;
④  为虚数单位,则
为虚数单位,则 .
.
正确命题的个数是( )
A. |
B.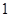 |
C. |
D.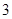 |
 的展开式的常数项是( )
的展开式的常数项是( )
| A.2 | B.3 | C.-2 | D.-3 |
已知身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )
| A.48种 | B.72种 | C.78种 | D.84种 |
同时抛掷三颗骰子一次,设 “三个点数都不相同”,
“三个点数都不相同”, “至少有一个6点”则
“至少有一个6点”则 为( )
为( )
A. |
B. |
C. |
D. |
方程 有三个不同的实根,则
有三个不同的实根,则 的取值范围是( )
的取值范围是( )
A.( ) ) |
B.( |
C. |
D. |
已知变量 和
和 满足关系
满足关系 ,变量
,变量 与
与 正相关. 下列结论中正确的是( )
正相关. 下列结论中正确的是( )
A. 与 与 负相关, 负相关, 与 与 负相关 负相关 |
B. 与 与 正相关, 正相关, 与 与 正相关 正相关 |
C. 与 与 正相关, 正相关, 与 与 负相关 负相关 |
D. 与 与 负相关, 负相关, 与 与 正相关 正相关 |
设 是虚数单位,则复数
是虚数单位,则复数 的共轭复数
的共轭复数 = .
= .
已知函数 在点P(1,m)处的切线方程为
在点P(1,m)处的切线方程为 ,则
,则 ________
________
设点 在
在 内部且满足
内部且满足 ,现将一粒豆子撒在
,现将一粒豆子撒在 中,则豆子落在
中,则豆子落在 内的概率是 .
内的概率是 .
由曲线 围成的封闭图形面积S= .
围成的封闭图形面积S= .
若多项式 ,则
,则 .
.
观察下列各式:




……
照此规律,当n N时,
N时,
 .
.
(本小题满分10分)已知复数
(1)求复数Z的模;
(2)若复数Z是方程 的一个根,求实数
的一个根,求实数 的值?
的值?
(本小题满分10分)万州区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ,
,
(本小题满分13分)某校高一年级开设 ,
, ,
, ,
, ,
, 五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选 课程,不选
课程,不选 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中 课程且乙同学未选中
课程且乙同学未选中 课程的概率;
课程的概率;
(Ⅱ)用 表示甲、乙、丙选中
表示甲、乙、丙选中 课程的人数之和,求
课程的人数之和,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)已知函数 .
.
(1)若 ,求
,求 的值域;
的值域;
(2)若存在实数t,当 ,
, 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.