复数 (
( 为虚数单位)的虚部是( )
为虚数单位)的虚部是( )
A. |
B. |
C. |
D. |
下列结论中正确的个数是( )
(1)在回归分析中,可用指数系数 的值判断模型的拟合效果,
的值判断模型的拟合效果, 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(2)在回归分析中,可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
(3)在回归分析中,可用相关系数 的值判断模型的拟合效果,
的值判断模型的拟合效果, 越小,模型的拟合效果越好;
越小,模型的拟合效果越好;
(4)在回归分析中,可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
| A.1 | B.2 | C.3 | D.4 |
下列推理是归纳推理的是( )
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,则P点的轨迹为椭圆 |
| B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜想出椭圆 + + =1的面积S=πab =1的面积S=πab |
| D.以上均不正确 |
某校为了研究学生的性别和对待某一活动的态度(支持和不支持两种态度)的关系,运用 列联表进行独立性检验,经计算
列联表进行独立性检验,经计算 ,则所得到的统计学结论是:有( )的把握认为“学生性别与支持该活动有关系”。
,则所得到的统计学结论是:有( )的把握认为“学生性别与支持该活动有关系”。
 |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
A、0.1% B、1% C、99% D、99.9%
设a,b是两个实数,给出下列条件:
①a+b>1;②a+b=2;③a+b>2;④a2+b2>2;⑤ab>1.
其中能推出:“a,b中至少有一个大于1”的条件是( )
| A.②③ | B.①②③ | C.③ | D.③④⑤ |
“因为指数函数y=ax是增函数,而 是指数函数,所以
是指数函数,所以 是增函数.”在以上三段论推理中( )
是增函数.”在以上三段论推理中( )
| A.大前提错误 |
| B.小前提错误 |
| C.推理形式错误 |
| D.大前提、小前提、推理形式错均正确 |
分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证 <
< a”索的因应是( )
a”索的因应是( )
| A.a-b>0 | B.a-c>0 |
| C.(a-b)(a-c)>0 | D.(a-b)(a-c)<0 |
阅读程序框图,若输入 ,则输出
,则输出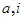 分别是( )
分别是( )

A.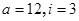 |
B.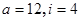 |
C.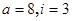 |
D.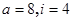 |
在复平面内,把复数3-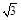 i对应的向量按顺时针方向旋转π/3,所得向量对应的复数是( )
i对应的向量按顺时针方向旋转π/3,所得向量对应的复数是( )
A.2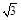 |
B.-2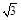 i i |
C.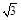 -3i -3i |
D.3+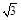 i i |
给出下列结论:在回归分析中可用
(1)可用相关指数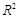 的值判断模型的拟合效果,
的值判断模型的拟合效果,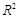 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(2)可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
(3)可用相关系数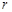 的值判断模型的拟合效果,
的值判断模型的拟合效果,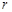 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(4)可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
以上结论中,正确的是( )
| A.(1)(3)(4) | B.(1)(4) |
| C.(2)(3)(4) | D.(1)(2)(3) |
在复平面内,复数 满足
满足 ,则
,则 对应点的坐标是 .
对应点的坐标是 .
将全体正整数排成一个三角形数阵:

按照以上排列的规律,第 行
行 从左向右的第5个数为 .
从左向右的第5个数为 .
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对应数据﹒
(吨标准煤)的几组对应数据﹒
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
m |
4 |
4.5 |
根据上表提供的数据,求出y关于x的线性回归方程 ,那么表中m的值为 .
,那么表中m的值为 .
为了判断高中学生选读文科是否与性别有关,现随机抽取50名学生,得到如下 列联表:
列联表:
| |
理科 |
文科 |
合计 |
| 男 |
13 |
10 |
23 |
| 女 |
7 |
20 |
27 |
| 合计 |
20 |
30 |
50 |
已知 ,
, ,根据表中数据,得到
,根据表中数据,得到 ,则在犯错误的概率不超过 的前提下可以认为选读文科与性别是有关系的。
,则在犯错误的概率不超过 的前提下可以认为选读文科与性别是有关系的。
用反证法证明命题:“设实数a、b、c满足a+b+c=1,则a、b、c中至少有一个数不小于 ”时,第一步应写:假设 .
”时,第一步应写:假设 .
已知等式“ ”、“
”、“ 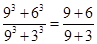 ”、“
”、“ 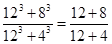 ”均成立.则
”均成立.则 .
.
已知a>0,b>0,m>0,n>0,求证:am+n+bm+n ≥ ambn+anbm.
已知关于x的方程:x2﹣(6+i)x+9+ai=0(a∈R)有实数根b.
(1)求实数a,b的值.
(2)若复数z满足| ﹣a﹣bi|﹣2|z|=0,求z为何值时,|z|有最小值,并求出|z|的值.
﹣a﹣bi|﹣2|z|=0,求z为何值时,|z|有最小值,并求出|z|的值.
为了解高二某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
下面的临界值表供参考:

(参考公式K2= ,其中n=a+b+c+d)
,其中n=a+b+c+d)
某地粮食需求量逐年上升,下表是部分统计数据:
| 年份(年) |
2002 |
2004 |
2006 |
2008 |
2010 |
| 需求量 (万吨) |
236 |
246 |
257 |
276 |
286 |
(1)利用所给数据求年需求量与年份之间的回归直线方程 =
= x+
x+ .
.
(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.