若(1+2ai)i=1-bi,其中a,b∈R,i是虚数单位,则|a+bi|=( )
A.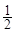 +i +i |
B.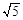 |
C. |
D. |
对于线性相关系数r,不列说法正确的是( )
A.|r| ,|r|越大,相关程度越大;反之相关程度越小 ,|r|越大,相关程度越大;反之相关程度越小 |
B.|r| ,|r|越大,相关程度越大;反之相关程度越小 ,|r|越大,相关程度越大;反之相关程度越小 |
C.|r| ,且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小 ,且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小 |
| D.以上说法都不正确 |
已知 的取值如下表所示
的取值如下表所示
 |
0 |
1 |
3 |
4 |
 |
2.2 |
4.3 |
4.8 |
6.7 |
从散点图分析 与
与 的线性关系,且
的线性关系,且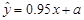 ,则
,则 ( )
( )
A.2.2 B.2.6 C.3.36 D.1.95
设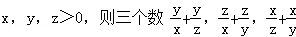 ( )
( )
| A.都大于2 |
| B.至少有一个大于2 |
| C.至少有一个不小于2 |
| D.至少有一个不大于2 |
下列表述正确的是( )
①归纳推理是由特殊到一般的推理;
②演绎推理是由一般到特殊的推理;
③类比推理是由特殊到一般的推理;
④分析法是一种间接证明法;
⑤若z∈C,且|z+2﹣2i|=1,则|z﹣2﹣2i|的最小值是3.
| A.①②③④ | B.②③④ | C.①②④⑤ | D.①②⑤ |
要证明 +
+ <2
<2 ,可选择的方法有以下几种,其中最合理的是( )
,可选择的方法有以下几种,其中最合理的是( )
| A.综合法 | B.分析法 | C.反证法 | D.归纳法 |
下列说法中正确的是( )
| A.合情推理就是类比推理 |
| B.归纳推理是从一般到特殊的推理 |
| C.合情推理就是归纳推理 |
| D.类比推理是从特殊到特殊的推理 |
若 是纯虚数(其中
是纯虚数(其中 是虚数单位),且
是虚数单位),且 ,则
,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
按下面的流程图进行计算.若输出的 ,则输入的正实数
,则输入的正实数 值的个数最多为( )
值的个数最多为( )

A. |
B. |
C. |
D. |
有一段 “三段论”推理是这样的:对于可导函数 ,若
,若 ,则
,则 是函数
是函数 的极值点.因为
的极值点.因为 在
在 处的导数值
处的导数值 ,所以
,所以 是
是 的极值点.以上推理中 ( )
的极值点.以上推理中 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
设复数 ,其中
,其中 为实数,若
为实数,若 的实部为2,则
的实部为2,则 的虚部为 .
的虚部为 .
用反证法证明命题:“如果a,b∈N,ab可被5整除,那么a,b中至少有一个能被5整除”时,假设的内容应为 .
一个车间为了规定工作定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:

由表中数据,求得线性回归方程 ,根据回归方程,
,根据回归方程,
预测加工70个零件所花费的时间为 分钟.
观察下列等式:
1=1,1-4=-(1+2),1-4+9=1+2+3,1-4+9-16=-(1+2+3+4),…由此推测第 个等式为 .(不必化简结果)
个等式为 .(不必化简结果)
用反证法证明命题:“若整数系数一元二次方程 有有理根,那么
有有理根,那么 中至少有一个是偶数”时,应假设 .
中至少有一个是偶数”时,应假设 .
按右边程序框图运算,若运算进行了3次才停止,则 的取值范围是 .
的取值范围是 .

(满分10分)(1)用分析法证明:当 时,
时, ;
;
(2)设 是两个不相等的正数,若
是两个不相等的正数,若 ,用综合法证明:
,用综合法证明:
(满分10分)已知复数 满足:
满足: 
(1)求 并求其在复平面上对应的点的坐标;
并求其在复平面上对应的点的坐标;
(2)求 的共轭复数E:\WCFUpload\Upload\2015-08\04\04891303-8df8-452b-8372-8b1d9afe39e5\ http:\\
的共轭复数E:\WCFUpload\Upload\2015-08\04\04891303-8df8-452b-8372-8b1d9afe39e5\ http:\\
(本小题满分13分)某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究,对该校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
(Ⅰ)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?
(Ⅱ)4名成员随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理。求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率。
 |
0.010 |
0.005 |
0.001 |
 |
6.635 |
7.879 |
10.828 |
附:
某单位为了了解用电量y度与气温x0C之间的关系随机统计了某4天的用电量与当天气温
| 气温(0C) |
14 |
12 |
8 |
6 |
| 用电量 |
22 |
26 |
34 |
38 |
(1)求用电量y与气温x的线性回归方程;
(2)由(1)的方程预测气温为50C时,用电量的度数。
参考公式:
