设集合
，集合
，则 
（ ）
A． |
B． |
C． |
D． |
已知平面向量
，
，
，
，
，
，若
，则实数
（ ）
| A．4 | B．－4 | C．8 | D．－8 |
设命题
：函数
在
上为增函数；命题
：函数
为奇函数．则
下列命题中真命题是（ ）
A． |
B． |
C． |
D． |
执行如图所示的程序框图，若输入的
，则输出的
属于（ ）
A． |
B． |
C． |
D． |
一个几何体的三视图中，正（主）视图和 侧(左)视图如图所示，则俯视图不可能为（ ）
某生产厂商更新设备，已知在未来
年内，此设备所花费的各种费用总和
（万元）与
满足函数关系
，若欲使此设备的年平均花费最低，则此设备的使用年限为（ ）
| A．3 | B．4 | C．5 | D．6 |
“
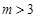”是“曲线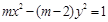
为双曲线”的（ ）
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
在长方体
中，
，
，点
为对角线
上的动点，点
为底面
上的动点（点，可以重合），则
的最小值为（ ）
A． |
B． |
C． |
D． |
复数
________．
抛物线
：
的准线
的方程是____；以
的焦点为圆心，且与直线相切的圆的方程是____．
设函数
， 则
____；函数
的值域是____．
在
中，角
，
，
所对的边分别为
，
，
， 若
，
，
，
则
____；的面积为____．
若
，
满足
，若
的最大值为
，则实数
____．
如图，正方形
的边长为2，
为
的中点，射线
从
出发，绕着点顺时针方向旋转至
，在旋转的过程中，记
为
，所经过的在正方形
内的区域（阴影部分）的面积
，那么对于函数
有以下三个结论：
①
；
②函数在
上为减函数；
③任意
，都有
；
其中所有正确结论的序号是________．
（本小题满分13 分）已知函数
．
（1）求函数
的定义域；
（2）求函数的单调增区间．
（本小题满分13分）设数列
的前n项和为
，且
，
．
（1）求数列的通项公式；
（2）若数列
为等差数列，且
，公差为
，当
时，比较
与
的大小．
（本小题满分14分）如图，在四棱锥
中，
，
平面
，
平面，
，
，
．
（1）求棱锥
的体积；
（2）求证：平面
平面
；
（3）在线段
上是否存在一点
,使
平面
？若存在,求出
的值；若不存在，说明理由．
（本小题满分13 分）某厂商调查甲、乙两种不同型号电视机在10 个卖场的销售量（单位：台），并根据这10个卖场的销售情况，得到如图所示的茎叶图．
为了鼓励卖场，在同型号电视机的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”．
（1）求在这10个卖场中，甲型号电视机的“星级卖场”的个数；
（2）若在这10个卖场中，乙型号电视机销售量的平均数为26．7，求
的概率；
（3）若
，记乙型号电视机销售量的方差为
，根据茎叶图推断
为何值时，达到最小值．（只需写出结论）
（注：方差
，其中
为
，
，…，
的平均数）
（本小题满分14 分）设
，
分别为椭圆
：
的左、右焦点，点
为椭圆的左顶点，点
为椭圆的上顶点，且
．
（1）若椭圆的离心率为
，求椭圆的方程；
（2）设
为椭圆上一点，且在第一象限内，直线
与
轴相交于点
，若以
为直径的圆经过点，证明：点在直线
上．
（本小题满分13分）已知函数
，其中
．
（1）当
时，求函数
的图象在点
处的切线方程；
（2）当
时，证明：存在实数
，使得对于任意的实数
，都有
成立；
（3）当
时，是否存在实数
，使得关于
的方程
仅有负实数解？当
时的情形又如何？(只需写出结论)．