某校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,
现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为( )
| A.45,75,15 | B.45,45,45 |
| C.30,90,15 | D.45,60,30 |
某程序框图如图所示,若输出的S=57,则判断框内为( ) 
| A.k>4? | B.k>5? | C.k>6? | D.k>7? |
在△ABC中,sin2A≤sin2B+sin2C-sinB sinC,则A的取值范围是( )
A. |
B. |
C.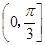 |
D.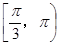 |
在等差数列{an}中,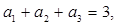
 ,则此数列前30项和等于( )
,则此数列前30项和等于( )
| A.810 | B.900 | C.870 | D.840 |
在△ABC中,角A,B,C所对的边分别为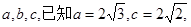 1+
1+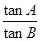 =
= ,则角C=( )
,则角C=( )
| A.30° | B.45° | C.45°或135° | D.60° |
等差数列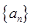 中,
中, 和
和 是关于方程
是关于方程 的两根,则该数列的前11项和
的两根,则该数列的前11项和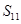 =( ).
=( ).
| A.58 | B.88 | C.143 | D.176 |
等差数列 的前
的前 项和为
项和为 .若
.若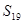 为一确定常数,下列各式也为确定常数的是
为一确定常数,下列各式也为确定常数的是
A. |
B.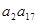 |
C.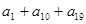 |
D. |
设 是满足
是满足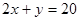 的正数,则
的正数,则 的最大值是( )
的最大值是( )
A. |
B.2 | C.50 | D.1 |
设等差数列 的前n项和为
的前n项和为 ,且满足
,且满足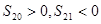 ,则
,则 中最大的项为( )
中最大的项为( )
A. |
B.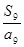 |
C. |
D. |
已知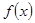 是定义在
是定义在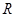 上的不恒为零的函数,且对于任意实数
上的不恒为零的函数,且对于任意实数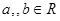 满足
满足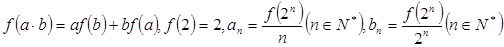
考察下列结论:
① ;
;
②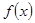 为偶函数;
为偶函数;
③ 数列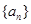 为等比数列;
为等比数列;
④ 数列 为等差数列.
为等差数列.
其中正确的结论是( )
| A.①②③ | B.②③④ | C.①②④ | D.①③④ |
北京2008年第29届奥运会开幕式上举行升旗仪式,在坡度15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为 米(如下图所示),则旗杆的高度为 米.
米(如下图所示),则旗杆的高度为 米.
数列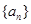 中,已知
中,已知 (
( 为常数)且
为常数)且 ,则
,则 ________.
________.
在△ABC中,B=60°,AC= ,则AB+2BC的最大值为________.
,则AB+2BC的最大值为________.
设数列 是等差数列,数列
是等差数列,数列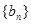 是等比数列,记数列
是等比数列,记数列 ,
,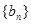 的前
的前 项和分别为
项和分别为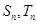 .若
.若 ,且
,且 ,则
,则 ________.
________.
在数列 中,已知
中,已知
(本小题满分12分)已知等差数列 的前
的前 项和
项和 满足
满足 ,
, .
.
(1)求 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和.
项和.
(本小题满分12分)已知
(本小题满分12分)等比数列 的前
的前 项和
项和 ,已知
,已知 ,且
,且 ,
, ,
,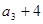 成等差数列.
成等差数列.
(1)求数列 的公比
的公比 和通项
和通项 ;
;
(2)若 是递增数列,令
是递增数列,令 ,求
,求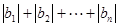 .
.
(本小题满分12分)在 中,角
中,角 的对边分别为
的对边分别为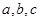 ,且
,且 .
.
(1)求 的值;
的值;
(2)若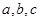 成等差数列,且公差大于0,求
成等差数列,且公差大于0,求 的值.
的值.
(本小题满分13分)已知数列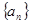 的前
的前 项和
项和 ,
, ,等差数列
,等差数列 中
中
(1)求数列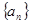 、
、 的通项公式;
的通项公式;
(2)是否存在正整数 ,使得
,使得 若存在,求出
若存在,求出 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
(本小题满分14分)已知数列 中,
中,
(1)令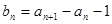 ,求证数列
,求证数列 是等比数列;
是等比数列;
(2)求数列 的通项;
的通项;
(3)设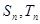 分别为数列
分别为数列
 的前
的前 项和,是否存在实数
项和,是否存在实数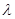 ,使得数列
,使得数列 为等差数列?若存在,试求出
为等差数列?若存在,试求出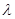 .若不存在,则说明理由.
.若不存在,则说明理由.